已知$O$为$\triangle ABC$的外心，且$\overrightarrow{BO}=\lambda\overrightarrow{BA}+\mu\overrightarrow{BC}$．
(1) 若$\angle C=90^\circ$，则$\lambda+\mu=$_______；
(2) 若$\angle ABC=60^\circ$，则$\lambda+\mu$的最大值为_______．
正确答案是$\dfrac{1}{2}$；$\dfrac{2}{3}$．
分析与解 (2)若$\angle ABC=60^\circ$，延长$BO$交$AC$于$D$，则\[\lambda+\mu=\dfrac{|BO|}{|BD|}\in\left(-\infty,\dfrac{2}{3}\right].\]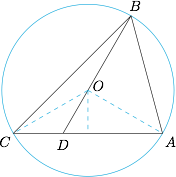
不妨设$\triangle ABC$的外接圆半径为$1$，根据向量线性分解的系数和的几何意义，有\[\lambda+\mu=\dfrac{OB}{BD}=\dfrac{OB}{OB+OD}\leqslant \dfrac{OB}{OB+d(O,AC)}=\dfrac{1}{1+\cos B}=\dfrac 23,\]因此$\lambda+\mu$的最大值为$\dfrac 23$．
附 首先，我们知道三点共线的向量表达：
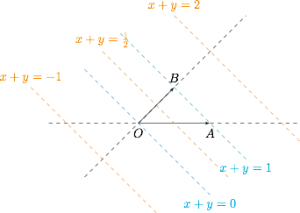
如果 $\overrightarrow{OA},\overrightarrow{OB}$ 是平面上的一组基底，且有 $\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$，那么“$x+y=1$”与“点 $C$ 位于直线 $AB$ 上”等价．
更进一步，有向量的等系数和线：
如果 $\overrightarrow{OA},\overrightarrow{OB}$ 是平面上的一组基底，且有 $\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$，若 $x+y=m$，那么 $\dfrac xm+\dfrac ym=1$，于是$$\overrightarrow{OC}=\dfrac xm\left(m\overrightarrow{OA}\right)+\dfrac ym\left(m\overrightarrow{OB}\right),$$记$$\overrightarrow{OP}=m\overrightarrow{OA},\overrightarrow{OQ}=m\overrightarrow{OB},$$则点 $C$ 位于直线 $PQ$ 上．
于是当向量分解的系数和$x+y$为定值时，点$C$的轨迹（$x,y$变化时）为一条与$AB$平行（或重合）的直线上，当$x+y$的值变化时，对应一系列平行的直线，即“向量分解的等系数和线”，如下图：