每日一题[825]对称化构造

已知$a>b>0$，$a^b=b^a$．

(1)求证：$a>{\rm e}>b>1$；

(2)求证：$a+b>2{\rm e}$；

(3)求证：$a\cdot b>{\rm e}^2$．

---

分析与证明　(1) 根据题意，有$\dfrac{\ln a}a=\dfrac{\ln b}b$．令$f(x)=\dfrac{\ln x}{x}$，则其导函数

$$f'(x)=\dfrac{1}{x^2}\cdot \left(1-\ln x\right),$$ 于是$f(x)$在$(0,{\rm e})$上单调递增，在$({\rm e},+\infty)$上单调递减，在$x={\rm e}$处取得极大值$\dfrac{1}{\rm e}$，如图．
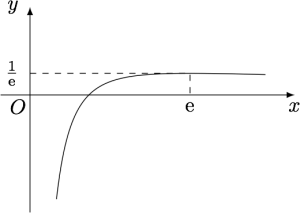因此可得$a>{\rm e}>b>1$．

(2) 显然只需要证明$a<2{\rm e}$的情形，即证明$b>2{\rm e}-a$，考虑到$b,2{\rm e}-a$均位于$f(x)$的单调递增区间$(0,{\rm e})$，因此只需要证明

$$f(b)>f(2{\rm e}-a),$$ 也即 $$f(a)>f(2{\rm e}-a).$$ 接下来我们证明 $$\forall x \in ({\rm e},2{\rm e}),f(x)-f(2{\rm e}-x)>0.$$ 设上述不等式左侧为$g(x)$，则其导函数 $$\begin{split}g'(x)&=f'(x)+f'(2{\rm e}-x)\\ &=\dfrac{1-\ln x}{x^2}+\dfrac{1-\ln (2{\rm e}-x)}{(2{\rm e}-x)^2}\\ &=\dfrac{1-\ln (2{\rm e}-x)}{(2{\rm e}-x)^2}-\dfrac{\ln x-1}{x^2}.\end{split}$$ 考虑到当$x \in ({\rm e},2{\rm e})$时，有 $$\ln x+\ln (2{\rm e}-x)=\ln [x\cdot (2{\rm e}-x)]<\ln{\rm e}^2=2,$$ 于是 $$1-\ln (2{\rm e}-x)>\ln x-1>0,$$ 又当$x \in ({\rm e},2{\rm e})$时，有 $$(2{\rm e}-x)^2<x^2,$$ 于是当$x \in ({\rm e},2{\rm e})$时，有$g'(x)>0$，因此$g(x)$在$({\rm e},2{\rm e})$上单调递增，结合$g({\rm e})=0$，命题得证．

(3) 显然只需要证明$a<{\rm e}^2$的情形，与(2)类似，只需要证明

$$\forall x>{\rm e},f(x)-f\left(\dfrac{{\rm e}^2}{x}\right)>0.$$ 设上述不等式左侧为$h(x)$，则其导函数 $$\begin{split}h'(x)&=f'(x)+\dfrac{{\rm e}^2}{x^2}\cdot f'\left(\dfrac{{\rm e}^2}{x}\right)\\&=\dfrac{1-\ln x}{x^2}+\dfrac{\ln x-1}{{\rm e}^2}\\&=\dfrac{(1-\ln x)({\rm e}-x)({\rm e}+x)}{{\rm e}^2x^2}\\&>0,\end{split}$$ 因此$h(x)$在$({\rm e},{\rm e}^2)$上单调递增，结合$h({\rm e})=0$，命题得证．