设函数$f(x)=\begin{cases} 2-|x+2|,x\leqslant 0,\\x^2,x>0,\end{cases} $,$g(x)=k\left(x-\dfrac 43\right)(k\in\mathbb{R})$,若存在唯一的整数$x$,使得$\dfrac{f(x)-g(x)}{x}<0$,则$k$的取值范围是________.
正确答案是$(-\infty,-3)\cup\left(-\dfrac 35,-\dfrac 37\right]$.
分析与解 先理解题中条件“存在唯一的整数$x$,使得$\dfrac{f(x)-g(x)}{x}<0$”:
这个条件等价于除了一个非零整数外,对所有其它整数均有$$\dfrac{f(x)-g(x)}{x}\geqslant 0,$$即对于一个非零整数外的其它整数均有$$\begin{cases} x>0,\\f(x)\geqslant g(x),\end{cases}\ \lor\ \begin{cases} x<0,\\f(x)\leqslant g(x).\end{cases} $$容易作出$f(x)$的图象,又$g(x)$的图象恒过点$\left(\dfrac 43,0\right)$,由$x<0$时,$f(x)\leqslant g(x)$对至多一个$x\in\mathbb{Z}$不成立知$k<0$:
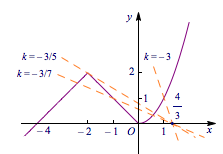
再结合$f(x)$的图象知,唯一的解只可能是$-2$或$1$,从而得到$k$的取值范围是$(-\infty,-3)\cup\left(-\dfrac 35,-\dfrac 37\right]$.

