每日一题[725]运动的向量

平面内向量$\overrightarrow a$，$\overrightarrow b$，$\overrightarrow c$满足$\Big|\overrightarrow a\Big|=\Big|\overrightarrow b\Big|=2$，$\Big|\overrightarrow c\Big|=1$，$\left(\overrightarrow a-\overrightarrow c\right)\cdot \left(\overrightarrow b-\overrightarrow c\right)=0$，则$\Big|\overrightarrow a-\overrightarrow b\Big|$的取值范围是_________．

---

分析与解　$\left[\sqrt 7-1,\sqrt 7+1\right]$．

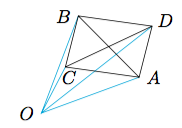
设$\overrightarrow a=\overrightarrow {OA}$，$\overrightarrow b=\overrightarrow {OB}$，$\overrightarrow c=\overrightarrow {OC}$，于是条件$(\overrightarrow c-\overrightarrow a)\cdot(\overrightarrow c-\overrightarrow b)=0$即

$$\overrightarrow {AC}\cdot\overrightarrow {BC}=0.$$ 将直角三角形$ABC$补成一个矩形$ACBD$，如图：

由矩形的性质知

$$OA^2+OB^2=OC^2+OD^2,$$ 即$8=1+OD^2$，解得$OD=\sqrt 7$．又因为$AB=CD=|\overrightarrow{a}-\overrightarrow{b}|$，所以 $$OD-OC=\sqrt 7-1\leqslant CD\leqslant OD+OC=\sqrt 7+1,$$ 等号可取到，所以所求范围为$[\sqrt 7-1,\sqrt 7+1]$．

另法　由题意知$A,B$在以$O$为圆心，$2$为半径的圆上运动；$C$在以$O$为圆心，$1$为半径的圆上运动，且有$AC\perp BC$，即点$C$在以$AB$为直径的圆上．$\Big|\overrightarrow a-\overrightarrow b\Big|=AB$，下面考虑$AB$长度的取值范围．

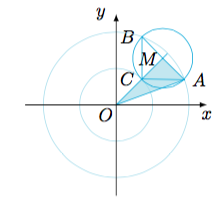
考虑点$M$在大圆$O$（半径为$2$的圆）的一条半径上运动，过$M$作$AB\perp OM$，与大圆相交于$A,B$两点，再以$M$为圆心，$\dfrac 12AB$为半径作圆$M$，若圆$M$与小圆$O$（半径为$1$的圆）有公共点，则对应的$A,B$满足要求．

于是得到两个临界情况，$AB$取到最小值时见下图左：

记$r=\dfrac 12AB$，在$\triangle OAM$中，有$r^2+(r+1)^2=2^2$，解得$r=\dfrac{\sqrt 7-1}{2}$．

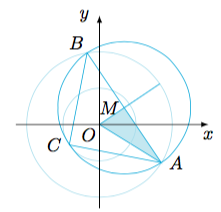
$AB$取到最大值时的情况见上图右．

在$\triangle OAM$中，有$r^2+(r-1)^2=2^2$，解得$r=\dfrac{\sqrt 7+1}{2}$，于是得到$AB=2r$的取值范围．