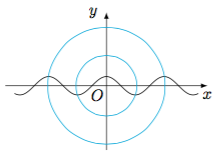
若存在实数$\varphi$,使圆面$x^2+y^2\leqslant 4$恰好覆盖函数$y=\sin\left(\dfrac{\pi}kx+\varphi\right)$的图象的最高或最低点共$3$个,则正实数$k$的取值范围是_______.
分析与解 由于$\varphi$控制着正弦型函数的图象的左右平移,因此我们思考一个与原题本质相同,但更容易理解的问题.
新问题 一个圆心在$x$轴上的圆面如果恰好覆盖$y=\cos x$的图象的最高或最低点共$3$个,那么它的半径的取值范围是多少?
不难知道,这个圆的半径的取值范围是$\left[\sqrt{\pi^2+1},\sqrt{4\pi^2+1}\right)$.回到原问题,当函数的最小正周期由$2\pi$变为$2k$时,可得$$\sqrt{k^2+1}\leqslant 2<\sqrt{4k^2+1},$$解得$k$的取值范围是$\left(\dfrac{\sqrt 3}2,\sqrt 3\right]$.