在$\triangle ABC$中，$AC=2AB=2$，$BC=\sqrt 3$，$P$是$\triangle ABC$内部一点，记$\triangle PAB,\triangle PBC,\triangle PCA$的面积分别为$S_{\triangle PAB},S_{\triangle PBC},S_{\triangle PCA}$，且$$\dfrac{S_{\triangle PAB}}{\overrightarrow {PA}\cdot \overrightarrow {PB}}=\dfrac{S_{\triangle PBC}}{\overrightarrow {PB}\cdot \overrightarrow {PC}}=\dfrac{S_{\triangle PCA}}{\overrightarrow {PC}\cdot \overrightarrow {PA}},$$则$PA+PB+PC=$________．
分析与解 $\sqrt 7$．
由题意知$$\dfrac {PA\cdot PB\cdot\sin\angle APB}{PA\cdot PB\cdot\cos\angle APB}=\dfrac {PB\cdot PC\cdot\sin\angle BPC}{PB\cdot PC\cdot\cos\angle BPC}=\dfrac {PC\cdot PA\cdot\sin\angle CPA}{PC\cdot PA\cdot\cos\angle CPA},$$于是有$$\tan\angle APB=\tan\angle BPC=\tan\angle CPA,$$从而有$$\angle APB=\angle BPC=\angle CPA=120^\circ.$$要求$PA+PB+PC$的值，我们希望将$PA,PB,PC$集中，将$\triangle BPC$绕$C$旋转$60$度(向点$A$对应的异侧旋转）得到$\triangle B'P'C$，如图：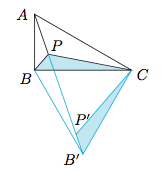
有$\triangle CPP',\triangle CBB'$为正三角形，从而有$$CP=PP',BP=B'P'.$$又因为$$\triangle APC+\angle CPP'=180^\circ=\angle PP'C+\angle CP'B',$$所以$A,P,P',B'$四点共线，从而$PA+PB+PC=AB'$．由题意知$\angle ACB=30^\circ$，所以$\triangle ACB'$为直角三角形，$AB'=\sqrt 7$即为所求．
事实上，点$P$是$\triangle ABC$的费马点，即是三角形$ABC$内到三个顶点的距离之和最小的点（证明过程同上）．