2013年北京市海淀区一模：
设$l_1,l_2,l_3$为空间中互相平行且两两间的距离分别为$4,5,6$的直线．给出下列三个结论：
(1) 存在$A_i\in l_i$($i=1,2,3$)，使得$\triangle A_1A_2A_3$是直角三角形；
(2) 存在$A_i \in l_i$($i=1,2,3$)，使得$\triangle A_1A_2A_3$是等边三角形；
(3) 三条直线上存在四点$A_i$($i=1,2,3,4$)，使得四面体$A_1A_2A_3A_4$为在一个顶点处的三条棱两两互相垂直的四面体．
其中，所有正确结论的序号是_______．
分析与解 如图，设直线$l_1,l_2,l_3$分别为“无底之直三棱柱”的三条“侧棱”$AD,BE,CF$，且平面$ABC$与侧棱垂直，$AB=4$，$BC=5$，$CA=6$．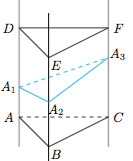
(1) 当$A_1=A,A_2=B,A_3=C$时，$\angle A_1A_2A_3<\dfrac{\pi}2$；当$A_1$向下运动，$A_3$向上运动时，$\angle A_1A_2A_3$趋于${\pi}$；因此必然在某个时刻$\angle A_1A_2A_3=\dfrac{\pi}2$，命题成立；
(2) 取$A_2=B$，$A_1$位于$A$点上方且$A_1A=3$，$A_3=C$，则$A_1A_2=A_2A_3=5$，$A_1A_3>6$，此时$\angle A_1A_2A_3>\dfrac{\pi}3$；让$A_1,A_3$同时向上运动，且保持$A_1A_2=A_3A_2$，则$\angle A_1A_2A_3$趋于$0$，必然存在某个时刻$\angle A_1A_2A_3=\dfrac{\pi}3$，命题成立；
(3) 显然四个点中有两个点位于同一条直线上，设为$A_1,A_2$，另外两点分别落在其他两条直线上．$A_3,A_4$显然不可能为直角顶点，因此$A_1$或$A_2$为直角顶点，不妨设$A_1$为直角顶点，则$A_3A_1\perp A_1A_2$，$A_4A_1\perp A_1A_2$，因此$\angle A_3A_1A_4$为二面角的平面角，且其大小与$\triangle ABC$的某个内角相同，不可能为$\dfrac{\pi}2$．因此不可能存在符合题意的四面体．
综上所述，命题(1)(2)正确．