已知空间四边形$ABCD$中，$AB=2$，$BC=8$，$CD=10$，$AD=4$，则$\overrightarrow {AC}\cdot \overrightarrow {BD}=$_______．
分析与解 在$\triangle ABC$中，我们根据余弦定理可得$$\begin{split} \overrightarrow {AB}\cdot \overrightarrow {AC}=&AB\cdot AC\cdot \cos A\\=&AB\cdot AC\cdot \dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\\=&\dfrac 12\left(AB^2+AC^2-BC^2\right).\end{split} $$因此在空间四边形$ABCD$中，我们有\[\begin{split} \overrightarrow {AC}\cdot \overrightarrow {BD}&=\overrightarrow {AC}\cdot \left(\overrightarrow {AD}-\overrightarrow {AB}\right)\\ &=\overrightarrow {AC}\cdot \overrightarrow {AD}-\overrightarrow {AC}\cdot \overrightarrow {AB}\\
&=\dfrac 12\left(AC^2+AD^2-CD^2\right)-\dfrac 12\left(AC^2+AB^2-BC^2\right)\\
&=\dfrac {\left(AD^2+BC^2\right)-\left(AB^2+CD^2\right)}2\\
&=-12.\end{split} \]
根据此题，我们有一般性的结论---空间余弦定理：
在空间四边形$ABCD$中，有$$\cos\langle AB,CD\rangle=\dfrac{\left|\left(AD^2+BC^2\right)-\left(AC^2+BD^2\right)\right|}{2\cdot AB\cdot CD}.$$特别的，可以得到$AD^2+BC^2=AC^2+BD^2$与$AB\perp CD$等价．
最后给出一道练习：
如图，在直三棱柱$ABC-A_1B_1C_1$中，$\angle BAC=\dfrac{\pi}2$，$AB=AC=AA_1=2$，点$G,E$分别为线段$A_1B_1,C_1C$的中点，点$D,F$分别为$AC,AB$上的动点，且$GD\perp EF$，则线段$DF$的长度的最小值是_____．
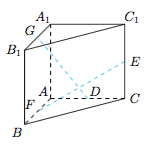解 根据空间余弦定理，由$GD\perp EF$，可得$$|FG|^2+|DE|^2=|GE|^2+|DF|^2,$$设$|AD|=a$，$|AF|=b$，则$$2^2+(1-b)^2+1^2+(2-a)^2=1^2+2^2+1^2+a^2+b^2,$$即$2a+b=2$，因此$$|DF|=\sqrt{a^2+b^2}=\dfrac{\sqrt{\left(a^2+b^2\right)\left(2^2+1^2\right)}}{\sqrt 5}\geqslant \dfrac{2a+b}{\sqrt 5}=\dfrac{2\sqrt 5}5,$$因此所求的最小值为$\dfrac{2\sqrt 5}5$．