每日一题[644]堪破玄机

已知椭圆$\dfrac{x^2}5+y^2=1$，过点$P(0,2)$的直线$l$交椭圆于$M,N$两点，若$\overrightarrow {PM}=\lambda\overrightarrow {PN}$，则$\lambda$的取值范围是______．

分析与解　当$M$在$P,N$之间时，作$M,N$在$y$轴上的投影$M_1,N_1$，则$\lambda =\dfrac{|PM_1|}{|PN_1|}$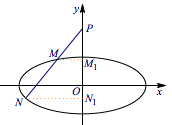：如图，当直线$l$的斜率增大时（由对称性知只需要考虑$M,N$在$y$轴一侧，包括轴上的情形即可），$|PM_1|$减小，$|PN_1|$增大，因此$\lambda $单调减小，显然其取值范围是$\left[\dfrac 13,1\right)$．

因此当$N$在$P,M$之间时，$\lambda$的取值范围是$\left(1,3\right]$，从而$\lambda$的取值范围是$\left[\dfrac 13,1\right)\cup\left(1,3\right]$．

说明　下面给出计算的方法：设直线$l$的方程为$y=kx+2$，与椭圆方程联立消元得$$\left(k^2+\dfrac 15\right )x^2+4kx+3=0,$$令$M,N$的横坐标分别为$x_1,x_2$，则有$\lambda =\dfrac {x_1}{x_2}$，则根据两根比公式得$$16k^2-\left(\lambda +\dfrac {1}{\lambda }+2\right )\cdot 3\left(k^2+\dfrac 15\right )=0$$整理得$$\lambda +\dfrac 1{\lambda }+2=\dfrac {16k^2}{3k^2+\dfrac 35}.$$由联立方程的判别式为正得到$k^2>\dfrac 35$，从而得到$$\dfrac {16k^2}{3k^2+\dfrac 35}\in \left(4,\dfrac {16}{3}\right ),$$即$2<\lambda +\dfrac 1{\lambda }<\dfrac {10}{3}$，解得$\dfrac 13<\lambda<3.$如果能看出两条线段长度的变化趋势，就可以直接得到本题的结果，避开复杂的计算．