每日一题[558]轨迹问题

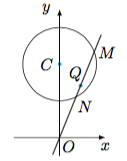
已知直线$l:y=kx$与圆$C:x^2+(y-4)^2=4$相交于$M,N$两点．

(1) 求$k$的取值范围；

(2) 若点$Q$在线段$MN$上，且满足$\dfrac{2}{|OQ|^2}=\dfrac{1}{|OM|^2}+\dfrac{1}{|ON|^2}$，求点$Q$的轨迹方程．

分析与解　(1) 根据题意，有$$\dfrac{4}{\sqrt{1+k^2}}<2,$$即$k^2>3$，于是$k$的取值范围是$(-\infty,-\sqrt 3)\cup (\sqrt 3,+\infty)$．

(2) 根据题意，由圆幂定理及垂径定理可得$$\begin{cases} |OM|\cdot |ON|=12,\\ |OM|+|ON|=2\cdot \dfrac{4|k|}{\sqrt{1+k^2}},\end{cases} $$于是$$\dfrac{2}{|OQ|^2}=\dfrac{(|OM|+|ON|)^2-2\cdot |OM|\cdot |ON|}{(|OM|\cdot |ON|)^2}=\dfrac{5k^2-3}{18(1+k^2)}.$$设$Q(x,y)$，则$k=\dfrac yx$($y>0$)，代入得$$\dfrac{2}{x^2+y^2}=\dfrac{5y^2-3x^2}{18(x^2+y^2)},$$化简得$$5y^2-3x^2=36,$$其中$\dfrac{y^2}{x^2}>3$，可得$x^2<3$且$x\neq 0$．从而所求点$Q$的轨迹方程为$$5y^2-3x^2=36(x^2<3,x\neq 0,y>0).$$

思考与总结　圆幂定理和垂径定理是直线与圆的位置关系问题中的重要定理，合理的运用这两个定理可以避开复杂的联立运算．