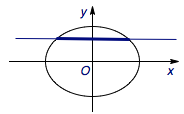
解不等式：\(\sqrt{x^2+4x+8}+\sqrt{x^2-4x+8}\leqslant 6\)．
原不等式即\[\sqrt{(x+2)^2+(2-0)^2}+\sqrt{(x-2)^2+(2-0)^2}\leqslant 6.\]
联想椭圆的定义，构造以\((-2,0)\)，\((2,0)\)为焦点，\(6\)为长轴长的椭圆\(\dfrac{x^2}{9}+\dfrac{y^2}{5}=1\)．
于是所求\(x\)的范围即直线\(y=2\)被椭圆截得的弦横坐标的取值范围，即\(\left[-\dfrac 3{\sqrt 5},\dfrac{3}{\sqrt 5}\right]\)．
下列给出一道练习题．
解方程：\(\left|3x-4\right|-\left|3x-8\right|=2\)．
提示 令\(3x-6=t\)，则方程变为\[|t+2|-|t-2|=2,\]于是\(t\)可以看作是双曲线\(x^2-\dfrac{y^2}3=1\)被\(x\)轴所截的交点的横坐标．