每日一题[483]函数的叠加

已知函数$f(x)=x^2\ln x+a(x^2-x)$($a>0$)，方程$f(x)=m$有两个不相等的实数根$x_1,x_2$，求证：$x_1+x_2>1$．

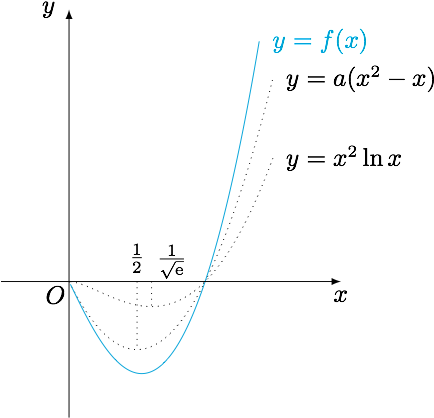
分析    函数$f(x)$由两个部分组成，其中函数$y=a(x^2-x)$的对称轴为$x=\dfrac 12$，而函数$y=x^2\ln x$，由于其导函数 $$y'=x(1+2\ln x),$$ 于是其极值点为$x=\dfrac{1}{\sqrt{\rm e}}$在$\dfrac 12$的右侧．因此合起来的函数$f(x)$的极值点应该会右移，可以从这个角度入手．

解    函数$f(x)$的导函数 $$f'(x)=2x\ln x+(2a+1)x-a,$$ 其二阶导函数 $$f''(x)=2\ln x+2a+3.$$ 注意到$f''(x)$单调递增有唯一零点，因此$f'(x)$先递减后递增．又考虑到 $$\lim\limits_{x\to 0} f'(x)=-a<0,f'(1)=a+1>0,$$ 因此函数$f'(x)$有唯一零点$x_0\in (0,1)$，且在$(0,x_0)$上有$f'(x)<0$，在$(x_0,+\infty)$上有$f'(x)>0$．进而$f(x)$先递减后递增，注意到 $$\lim\limits_{x\to 0}f(x)=0,f(1)=0,$$ 因此函数图象如图．由于 $$f'\left(\dfrac 12\right)=\dfrac 12+\ln\dfrac 12<0,$$ 于是$f(x)$在$\left(0,\dfrac 12\right]$上单调递减，不妨设$x_1<x_2$，则有$0<x_1<x_2<1$且$x_2>\dfrac 12$．

第一种情况，$\dfrac 12\leqslant x_1<x_2<1$，此时命题显然成立；

第二种情况，$0<x_1<\dfrac 12< x_2<1$．对称化构造函数，接下来证明辅助命题 $$\forall x\in\left(\dfrac 12,1\right),f(x)< f(1-x),$$ 即 $$\forall  x\in\left(\dfrac 12,1\right),x^2\ln x-(1-x)^2\ln (1-x)<0.$$ 设$g(x)=x^2\ln x-(1-x)^2\ln (1-x)$，则其导函数 $$g'(x)=1+2x\ln x+2(1-x)\ln (1-x),$$ 其二阶导函数 $$g''(x)=2\ln x-2\ln(1-x)\geqslant 0,$$ 于是$g'(x)$单调递增，考虑到 $$g'\left(\dfrac 12\right)<0,\lim\limits_{x\to 1}g'(x)=1,$$ 于是$g(x)$在$\left(\dfrac 12,1\right)$上先单调递减，再单调递增，又 $$g\left(\dfrac 12\right)=0,\lim\limits_{x\to 1}g(x)=0,$$ 因此$g(x)$在$\left(\dfrac 12,1\right)$上有$g(x)< 0$，也即辅助命题得证．

应用辅助命题，有 $$f(x_1)=f(x_2)< f(1-x_2),$$ 而$x_1,1-x_2\in\left(0,\dfrac 12\right)$，而$f(x)$在$\left(0,\dfrac 12\right)$上单调递减，从而 $$x_1> 1-x_2,$$ 即 $$x_1+x_2> 1.$$

综上所述，原命题得证．