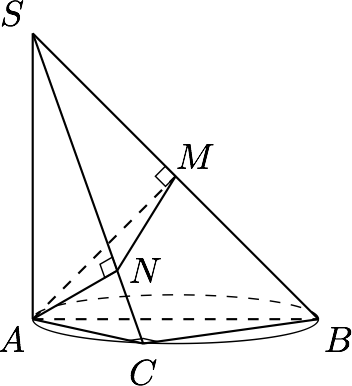
如图,$AB$是圆$O$的直径,$SA$与圆$O$所在的平面垂直且$SA=AB=2$.$C$为圆$O$上不同于$A,B$的点,$M,N$分别为$A$在线段$SB,SC$上的投影.当三棱锥$S-AMN$的体积最大时,$SC$与平面$ABC$所成角的正弦值是_______.
分析 显然$M$点为定点(线段$SB$的中点),因此问题的关键在于确定$N$点的轨迹.
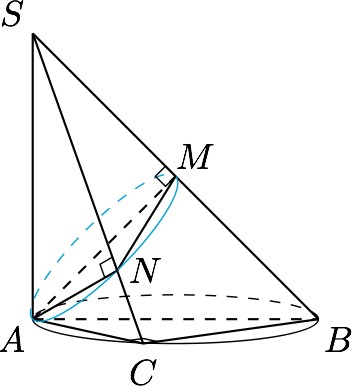
解 根据题意有\[\left.\begin{split}\left.\begin{split} SA\perp BC \\ AC\perp BC\end{split}\right\}\Rightarrow BC\perp SAC\Rightarrow BC\perp AN \\ SC\perp AN\end{split} \right\}\Rightarrow AN\perp SBC,\]因此$AN\perp NM$,即$N$点的轨迹是以$AM$为直径的圆(不包含$A,M$两点),如图.
此时三棱锥$S-AMN$的体积$$V=\dfrac 16 AN\cdot NM\cdot SM=\dfrac{\sqrt 2}6\cdot AN\cdot NM,$$且$$AN^2+NM^2=AM^2=2,$$于是当$AN=NM=1$时,三棱锥$S-AMN$的体积最大,此时$\angle ASN=\dfrac{\pi}6$,因此所求正弦值为$\cos\dfrac{\pi}6=\dfrac{\sqrt 3}2$.
注 有趣的是,当$C$在圆上运动时,$N$也在圆上运动;$SA,AC,CB$两两垂直,$AN,NM,MS$也两两垂直.因此三棱锥$S-ABC$与三棱锥$S-MAN$是类似的,这个作图过程可以无限进行下去.