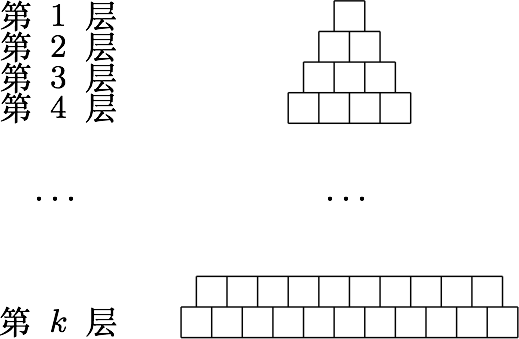
如图,由若干个小正方形组成的$k$层三角形图阵,第一层有$1$个小正方形,第二层有$2$个小正方形,依此类推,第$k$层有$k$个小正方形.除去最底下一层,每个小正方形都放置在它下一层的两个小正方形之上.现对第$k$层的每个小正方形用数字进行标注,从左到右依次记为$x_1,x_2,\cdots ,x_k$,其中$x_i\in\{0,1\}$($1\leqslant i\leqslant k$),其它小正方形标注的数字是它下面的两个小正方形标注的数字之和,依此规律,记第一层的小正方形标注的数字为$x_0$.
(1)当$k=4$时,若要求$x_0$为$2$的倍数,则有多少种不同的标注方法?
(2)当$k=11$时,若要求$x_0$为$3$的倍数,则有多少种不同的标注方法?
分析与解 (1)类似于杨辉三角,我们容易知道$$x_0={\rm C}_{k-1}^{0}x_1+{\rm C}_{k-1}^{1}x_2+{\rm C}_{k-1}^{2}x_3+\cdots +{\rm C}_{k-1}^{k-1}x_k.$$如图为$k=4$时每个方格中的数加的次数.
这样,我们就可以得到不同的标注方法数为$${\rm C}_4^0+{\rm C}_4^2+{\rm C}_4^4=8.$$
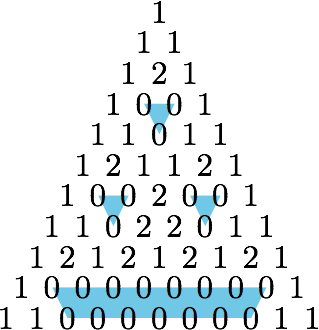
(2)从第(1)小题的解决中可以看到,第$k$层各个方格中的数字本身可以替换为对应的模同余的余数.因此,当$k=11$时,可以如图填数.
这样,我们就可以得到不同的标注方法数为$$\left({\rm C}_4^0+{\rm C}_4^3\right)\cdot 2^7=640.$$
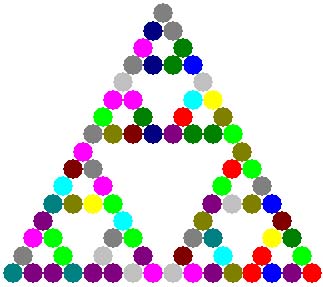
注 如果把新的“杨辉三角”中所有的$0$用特别的颜色标记出来,就会得到类似于谢尔宾斯基三角的美丽图案.