在平面直角坐标系中,已知点$F(3,0)$在圆$C:(x-m)^2+(y-2)^2=40$内,动直线$AB$过点$F$且交圆于$A,B$两点,若$\triangle ABC$的面积的最大值为$20$,则实数$m$的取值范围是_______.
正确答案是$(-3,-1]\cup [7,9)$.
分析 在解直线与圆的题目时,以下几何量知其二就能推出其他几何量:
① 半径$r$;
② 弦所对的圆心角或圆周角$\theta$;
③ 弦长$l$;
④ 弦心距$d$.
另一方面,弦的两个端点与圆心构成的三角形的面积可以由①②计算,也可以由③④计算,这些几何量之间的关系是需要在计算中熟练应用的.
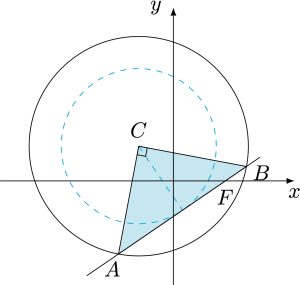
解 注意到$\triangle ABC$是以弦$AB$为底,圆$C$的半径为腰的等腰三角形.于是可得当$\triangle ABC$的面积取得最大值$20$时,其顶角$\angle ACB$为直角,进而将条件“挪移”为圆心$C$到直线$AB$的距离为半径的$\dfrac{1}{\sqrt 2}$,也即直线$AB$是圆$$(x-m)^2+(y-2)^2=20$$的切线,如图.
因此题意即过点$F$可以作圆$$(x-m)^2+(y-2)^2=20$$的切线,即$$20\leqslant (3-m)^2+(0-2)^2<40,$$解得$m$的取值范围是$(-3,-1]\cup [7,9)$.