这是2012年北京市西城区的一道高考模拟题：
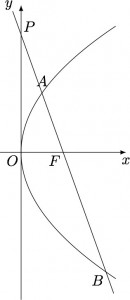
已知抛物线$y^2=2px$($p>0$)的焦点为$F$，过点$F$的直线交$y$轴正半轴于点$P$，交抛物线于$A,B$两点，其中点$A$在第一象限．
(I)求证：以线段$FA$为直径的圆与$y$轴相切；
(II)若$\overrightarrow{FA}=\lambda_1\overrightarrow{AP}$，$\overrightarrow{BF}=\lambda_2\overrightarrow{FA}$，$\dfrac{\lambda_1}{\lambda_2}\in\left[\dfrac 14,\dfrac 12\right]$，求$\lambda_2$的取值范围．
分析 第(I)小题只需要证明$$\dfrac{x_A+x_F}2=\dfrac 12|AF|$$即可．实际上，由抛物线的定义易得．
第(II)小题引入了两个参数$\lambda_1$和$\lambda_2$，使得题目蕴含更多的“变数”．看似“东南西北”纷繁复杂，实则是对多参数问题的代数处理能力的一次考量．事实上，以$A,B$两点的坐标参数为基本参数，注意齐次特性用$\lambda_2$表示$\lambda_1$即可．
解答 (I)略；
(II)设$A(2pt_1^2,2pt_1)$，$B(2pt_2^2,2pt_2)$，$P(0,m)$，则由直线$AB$与直线$PA$的斜率相等得$$\dfrac{m-2pt_1}{0-2pt_1^2}=\dfrac{2pt_1-2pt_2}{2pt_1^2-2pt_2^2},$$解得$$m=\dfrac {2pt_1t_2}{t_1+t_2}.$$这样我们有$$\lambda_2=-\dfrac{t_2}{t_1},$$其中$\lambda_2>1$．进而$$\lambda_1=\dfrac{2pt_1}{\dfrac{2pt_1t_2}{t_1+t_2}-2pt_1}=-1-\dfrac{t_2}{t_1}=-1+\lambda_2,$$因此根据题意有$$\dfrac{-1+\lambda_2}{\lambda_2}\in\left[\dfrac 14,\dfrac 12\right],$$解得$\lambda_2$的取值范围是$\left[\dfrac 43,2\right]$．
注 事实上，根据抛物线的几何平均性质，有$$2pt_1^2\cdot 2pt_2^2=\left(\dfrac p2\right)^2,$$从而$$t_1t_2=-\dfrac 14.$$但是对于本题而言，直线$AB$过点$F$的条件是多余的．