已知函数$f(x)=\begin{cases} 1,x\in\mathcal{Q},\\0,x\in\complement_{\mathcal {R}}{\mathcal {Q}}.\end{cases} $,给出下列三个命题:
①函数$f(x)$为偶函数;
②存在$x_i\in\mathcal{R}(i=1,2,3)$,使得以点$(x_i,f(x_i))(i=1,2,3)$为顶点的三角形是等腰直角三角形;
③存在$x_i\in\mathcal{R}(i=1,2,3,4)$,使得以点$(x_i,f(x_i))(i=1,2,3,4)$为顶点的四边形是菱形.
其中,所有真命题的序号是____.
正确答案是①③.
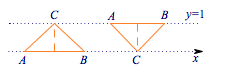
解 显然①正确,下面考虑②③,我们无法画出函数$f(x)$的图象,但这个图象上所有的点都在直线$y=1$与$x$轴上,对于②,一方面因为三个点中至少有两个点纵坐标相同,所以直角三角形至少有一条边与$x$轴平行;另一方面由函数的定义知,直角边不可能与$x$轴垂直,所以直角边不可能与$x$轴平行,从而斜边必与$x$轴平行,于是只可能是如下图的两种情况:
易知,这三个点的横坐标分别相差$1$,所以它们的坐标只可能全为有理数或全为无理数,故不存在满足条件的三角形;
对于③,如图,需要点$A,B$的横坐标为无理数,点$C,D$的横坐标为有理数,
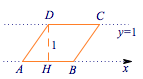
从而$AH$的长为无理数,而$AD=CD$为有理数,可以令$AH=\sqrt 3$,令$H(1,0)$,从而有$D(1,1),C(3,1),A(1-\sqrt 3,0),B(3-\sqrt 3,0)$,故满足条件的菱形存在.
类似地,大家可以思考,能否找到等边三角形?能否找到直角三角形?
题目中的函数就是著名的狄利克莱函数,它有很多不同寻常的性质,比如它是周期函数,且所有的非零有理数都是它的周期,但是它没有最小正周期.它的图象是客观存在的,但是无法画出;同时,它还是一个处处都不连续的函数.