每日一题[348]沟通的桥梁

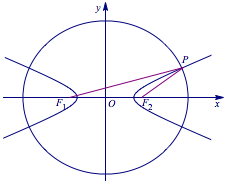
已知有公共焦点的椭圆与双曲线中心为原点，焦点在$x$轴上，左右焦点分别为$F_1,F_2$，且它们在第一象限的交点为$P$，$\triangle PF_1F_2$是以$PF_1$为底边的等腰三角形，若双曲线的离心率的取值范围为$(1,2)$，则该椭圆的离心率的取值范围是_____．

---

正确答案是$\left(\dfrac 13,\dfrac 25\right )$．

解　本题中椭圆与双曲线的半焦距长相等，设为$c$，设椭圆的长半轴长为$a_1$，离心率为$e_1$，双曲线的实半轴长为$a_2$，离心率为$e_2$．因为点$P$同时在椭圆与双曲线上，所以根据椭圆与双曲线的定义，我们就可以得到$\triangle PF_1F_2$的边长的多个关系式，进而得到$a_1,a_2,c$的联系，导出离心率$e_1,e_2$的大小关系，得到结论．如图：

设$|PF_1|=2m$，$|PF_2|=2n$，由椭圆与双曲线的定义知

$$2m+2n=2a_1,2m-2n=2a_2,2n=2c,$$ 从而有 $$n=c,a_1=m+c,a_2=m-c.$$ 于是有 $$e_1=\dfrac {c}{m+c},e_2=\dfrac {c}{m-c}.$$ 从而得到$\dfrac {1}{e_1}-\dfrac {1}{e_2}=2$，由$e_2\in(1,2)$得到$e_1\in\left(\dfrac 13,\dfrac 25\right )$．

---

下面给出一道练习：

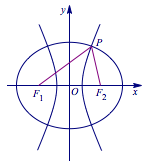
已知有公共焦点的椭圆与双曲线中心为原点，焦点在$x$轴上，左右焦点分别为$F_1,F_2$，且它们在第一象限的交点为$P$，$\triangle PF_1F_2$是以$PF_2$为底边的等腰三角形，若双曲线的离心率的取值范围为$(1,2)$，则该椭圆的离心率的取值范围是_____．

答案　$\left(\dfrac 23,1\right )$．

提示　如图，由椭圆与双曲线的定义可以得到$\dfrac {1}{e_1}+\dfrac {1}{e_2}=2.$