已知向量\(\left|\overrightarrow a\right|=\left|\overrightarrow b\right|=2\),\(\left|\overrightarrow c\right|=1\),$(\overrightarrow c-\overrightarrow a)\cdot(\overrightarrow c-\overrightarrow b)=0$,则\(\overrightarrow a\cdot \overrightarrow b\)的取值范围是____.
正确答案是$[-\sqrt 7,\sqrt 7]$.
解 思路一 几何角度
设\(\overrightarrow a=\overrightarrow {OA}\),\(\overrightarrow b=\overrightarrow {OB}\),\(\overrightarrow c=\overrightarrow {OC}\),于是条件$$(\overrightarrow c-\overrightarrow a)\cdot(\overrightarrow c-\overrightarrow b)=0$$即$$\overrightarrow {AC}\cdot\overrightarrow {BC}=0.$$
由题意知$A,B$在以$O$为圆心,$2$为半径的圆上运动;$C$在以$O$为圆心,$1$为半径的圆上运动,且有$AC\perp BC$,即点$C$在以$AB$为直径的圆上.
记$AB$的中点为$M$,有$$\overrightarrow a\cdot\overrightarrow b=OM^2-\dfrac 14AB^2,$$所以要求$\overrightarrow a\cdot \overrightarrow b$的范围,只需要求出$AB$的范围即可.
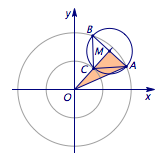
因为$OM\perp AB$,考虑点$M$为大圆$O$(半径为$2$的圆)的一条半径上的动点,过$M$作$AB\perp OM$,于大圆交于$A,B$两点,再以$M$为圆心,$\dfrac 12AB$为半径作圆$M$,若圆$M$与小圆$O$(半径为$1$的圆)有公共点,则对应的$A,B$满足要求,如图:
于是得到两个临界情况,下图是$AB$取到最小值时情况:
记$r=\dfrac 12AB$,在$\triangle OAM$中,有$$r^2+(r+1)^2=2^2,$$解得$$r=\dfrac{\sqrt 7-1}{2}.$$
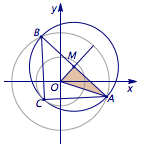
下图是$AB$取到最大值时的情况:
在$\triangle OAM$中,有$$r^2+(r-1)^2=2^2,$$解得$$r=\dfrac{\sqrt 7+1}{2}.$$
于是得到$\overrightarrow a\cdot\overrightarrow b$的取值范围.
思路二 代数角度
将条件$$(\overrightarrow c-\overrightarrow a)\cdot(\overrightarrow c-\overrightarrow b)=0$$整理得\[1-(\overrightarrow a+\overrightarrow b)\cdot \overrightarrow c+\overrightarrow a\cdot \overrightarrow b=0,\]所以\[(\overrightarrow a+\overrightarrow b)\cdot \overrightarrow c=1+\overrightarrow a\cdot \overrightarrow b.\]设\(\overrightarrow a\cdot \overrightarrow b=x\),\(\theta =\langle\overrightarrow a+\overrightarrow b,\overrightarrow c \rangle\),则\[\left|\overrightarrow a+\overrightarrow b\right|=\sqrt{(\overrightarrow a+\overrightarrow b)^2}=\sqrt{8+2x}.\]所以\[\sqrt{8+2x}\cdot 1 \cdot \cos \theta=1+x,\]得到\[-1\leqslant \dfrac{1+x}{\sqrt{8+2x}}\leqslant 1.\]即\[(1+x)^2\leqslant 8+2x,\]解得\[-\sqrt 7\leqslant x\leqslant \sqrt 7.\]
向量具有两面性,向量相关的问题既可以从几何角度出发,将向量对应到有向线段中,通过向量运算的几何意义进行求解,此时要注意选择合适的起点,灵活运用向量的换底公式;也可以通过代数角度,直接利用运算规律对条件进行分析与化简,或者建系后进行坐标运算.
更多向量相关的问题见每日一题[208]数量积的范围、每日一题[113]平面向量的“积化和差”.