从本质角度理解函数的性质

函数的性质本质上指当自变量满足某些关系时，函数值是否随之满足某些关系．具有某种性质的函数，会同时反应在函数的解析式与函数的图象上，借助于性质的本质，解析式满足的关系与图象满足的特征之间可以很好地对应起来．

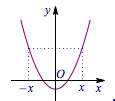
以偶函数为例，若函数\(f(x)\)是偶函数，那么它的解析式满足方程\(f(-x)=f(x)\)，它的图象关于\(y\)轴对称．从偶函数本质上理解：当两个自变量的和为\(0\)时，对应的函数值相等，这两个点也恰好关于\(y\)轴对称，如图：

如果一个函数\(f(x)\)满足对定义域内任意一个\(x\)，都有\[f(x+1)=f(-x-1)，\]那么函数\(f(x)\)具有什么性质，图象具有什么特点呢？

从形式上看，这与偶函数的定义不一样，但从本质上来看，仍然满足当自变量的和为\(0\)时，函数值相等，所以\(f(x)\)仍然为偶函数．

事实上，令\(t=x+1\)，则我们得到\(f(t)=f(-t)\).

从这个角度出发，我们可以推导，如果函数\(y=f(x)\)的图象关于直线\(x=2\)对称，\(f(x)\)的解析式满足的方程．

推导　图象关于\(x=2\)对称，意味着自变量的和为\(4\)时，函数值相等，所以有\[f(x)=f(4-x)，\]如果你愿意，也可以写成\[f(x+1)=f(3-x),\]甚至\[f(2x-1)=f(5-2x)，\]因为这些方程都可以导出当自变量的和为\(4\)时，函数值相等．

解析式满足的关系式可以从形式上千变万化，但从本质上始终保持一致．抓住性质的本质就可以以不变应万变．

根据上面的思路，由奇函数的定义\(f(x)+f(-x)=0\)，很容易得到奇函数的本质：当自变量的和为\(0\)时，函数值的和也为\(0\)．由此可以推导与中心对称相关的性质．比如：

若函数\(y=f(x)\)满足：\(f(x+1)+f(-x+1)=0\)，那么\(y=f(x)\)关于\((1,0)\)中心对称，因为当自变量的和为\(2\)时，函数值的和为\(0\)．

若函数\(y=f(x)\)的图象关于点\((1,2)\)中心对称，则有\[f(x)+f(2-x)=4.\]

下面看一个用性质的本质去推导的例子：

求证　如果一个函数有双对称轴，那么它一定是周期函数．

不妨以特殊的函数为例进行证明，若函数\(y=f(x)\)的图象关于\(x=1\)与\(x=2\)对称，证明\(f(x)\)是周期函数，并求出它的一个周期．

证　由\(y=f(x)\)的图象关于\(x=1\)对称知，当自变量和为\(2\)时，函数值相等，即\[f(x)=f(2-x).\]同理有\[f(x)=f(4-x).\]于是我们得到\[f(2-x)=f(4-x)．\]这说明当自变量相差\(2\)时，函数值相等，这是周期性的本质，故\(y=f(x)\)是周期函数，\(2\)是它的一个周期．

最后我们给出一道练习（2009年高考数学全国I卷理科第11题）

函数\(f(x)\)的定义域为\(\mathcal{R}\)，若\(f(x+1)\)与\(f(x-1)\)都是奇函数，则（　　）

A．\(f(x)\)是偶函数

B．\(f(x)\)是奇函数

C．\(f(x)=f(x+2)\)

D．\(f(x+3)\)是奇函数

答案　D

提示：令\(g(x)=f(x+1)\)，由\(g(-x)+g(x)=0\)知\(f(-x+1)+f(x+1)=0\)，即\[f(x)=-f(2-x).\]同理有\[f(x)=-f(-2-x).\]从而有\[f(2-x)=f(-2-x),\]得到\(f(x)\)是周期为\(4\)的函数，从而\(f(x+3)=f(x-1)\)为奇函数．

---

注　除了从性质的本质角度出发外，利用图象的变换也是一个可以尝试的角度，但有一定的局限性．比如，若\(y=f(x)\)的图象关于\(x=2\)对称知，我们推导\(f(x)\)满足的方程．将\(y=f(x)\)的图象向左平移两个单位后，得到的函数的图象关于\(y\)轴对称，即\(y=f(x+2)\)是一个偶函数．记\(g(x)=f(x+2)\)，有\(g(-x)=g(x)\)，从而\[f(-x+2)=f(x+2)．\]