已知平面\(\alpha\)和\(\beta\)相交形成的四个二面角中的其中一个为\(60^\circ\),则在空间中过某定点\(P\)与这两个平面所成的线面角均为\(30^\circ\)的直线\(l\)条数为_______.
正确答案是\(3\).
解 我们知道,研究空间的角度问题时,平面与其他空间图形所成的角度往往依托其法线进行计算.换句话说,平面的法线是平面方向的代表.
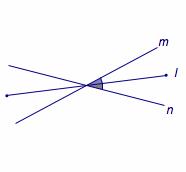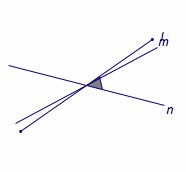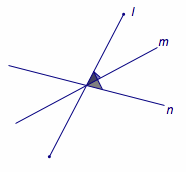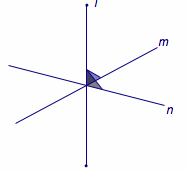
在这个问题中,设平面\(\alpha\)与平面\(\beta\)过\(P\)点的法线分别为\(m\)、\(n\),则\(\langle m,n\rangle=60^\circ\).而此时条件直线\(l\)与两个平面所成的线面角为\(30^\circ\)可以转化为直线\(l\)与直线\(m\)、\(n\)所成的角均为\(60^\circ\).
如图,平面上的两条直线(所成角为\(\theta\))的平分线——为互相垂直的两条直线——在运动过程中始终保持与两条直线所成的角相等,且该角的取值范围分别为\(\left[\dfrac{\theta}2,\dfrac{\pi}2\right]\)以及\(\left[\dfrac{\pi -\theta}2,\dfrac{\pi}2\right]\).
因此当\(\theta=60^\circ\),而与两条直线所成角均为\(60^\circ\)时对应的直线为\(3\)条.
下面给出一个练习题.
将一个水平放置的正方形\(ABCD\)绕直线\(AB\)向上转动\(45^\circ\)到\(ABC_1D_1\),再将所得正方形\(ABC_1D_1\)绕直线\(BC_1\)向上转动\(45^\circ\)到\(A_2BC_1D_2\),则平面\(A_2BC_1D_2\)与平面\(ABCD\)所成二面角的正弦值是_______.(\(\dfrac{\sqrt 3}2\))
提示 可以化为法线问题后应用三射线定理,可以参考 每日一题[46]三射线定理,以及 每日一题[202] 又见三射线定理.