每日一题[212] 困兽犹斗

2014年全国高中数学联赛四川省预赛第9题：

已知$a,b$为实数，对任何满足$0\leqslant x\leqslant 1$的实数$x$，都有$\left|ax+b\right|\leqslant 1$成立，则$\left|20a+14b\right|+\left|20a-14b\right|$的最大值是_______．

正确答案是$80$．

我们熟知 $$\left|20a+14b\right|+\left|20a-14b\right|=\max\left\{40|a|,28|b|\right\},$$ 于是问题转化为求$|a|$、$|b|$的最大值．

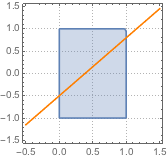
当$x=0$时，容易得到 $$|b|\leqslant 1,$$ 而由图可知被困在矩形区域的直线$f(x)=ax+b$在$x\in [0,1]$上的值域为$[-1,1]$的子集，于是斜率$a$必然在$[-2,2]$内，于是 $$|a|\leqslant 2,$$ 从而不难得到当$a=2\land b=-1$时，原式取得最大值为$80$．

事实上，依照图形的启示，对$|a|\leqslant 2$的严格表述可以利用$f(0)=|b|$和$f(1)=|a+b|$进行： $$|a|=\left|\left(a+b\right)-b\right|\leqslant |a+b|+|b|\leqslant 2.$$

下面这个问题可以作为练习：

若对任何满足$-1\leqslant x\leqslant 1$的实数$x$，都有$\left|ax^2+bx+c\right|\leqslant 1$成立，求$a$的取值范围．

答案是$-2\leqslant a\leqslant 2$，如图．