台球桌上的几何学

其实我不太了解台球，只知道有个号称九球皇后的“小潘婷”潘晓婷．

言归正传，分享两道高考题，你就会明白台球桌上的技术是如何帮助我们解题的．

第一道题是2012年全国卷（理）的第12题：

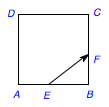
正方形$ABCD$的边长为$1$，点$E$在边$AB$上，点$F$在边$BC$上，$AE=BF=\dfrac 37$，动点$P$从$E$出发沿直线向$F$运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角，当点$P$第一次碰到$E$时，$P$与正方形的边碰撞的次数为（        ）

A．16

B．14

C．12

D．10

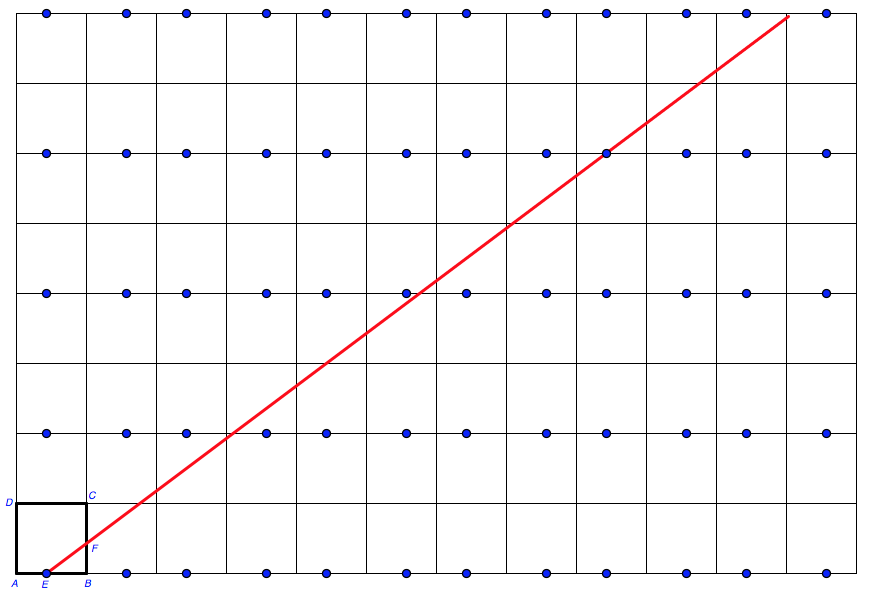
想象一下，如果我们不去反射动点的轨迹，而让动点沿射线运动，那么此时正方形就会不停地进行反射．

此时，点$E$会有无数个影子，射线$EF$击中的第一个影子就对应着“点$P$第一次碰到$E$”．可以用代数的方法进行分析，以$A$为原点，建立平面直角坐标系，则$E$及它的影子的坐标形如$\left(2m\pm\dfrac 37,2n\right)$，其中$m,n\in\mathcal Z$．初始的点$E\left(\dfrac 37,0\right)$，$F\left(1,\dfrac 37\right)$，因此

$$\dfrac {2n-0}{2m\pm \dfrac 37-\dfrac 37}=\dfrac {\dfrac 37-0}{1-\dfrac 37}.$$

其最小的正整数解$(m,n)$为$(4,3)$．

事实上，$m$或$n$每增加$1$，都会引起$2$次的“穿越”（也就是真实环境中的“反射”），因此所求的次数为$2(m+n)=14$．

---

第二道题是2014年江西卷（理）第10题：

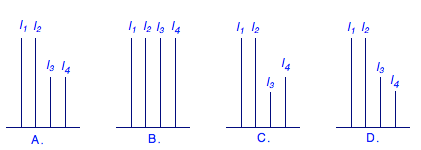
在长方体$ABCD-A_1B_1C_1D_1$中，$AB=11$，$AD=7$，$AA_1=12$，一质点从顶点$A$射向点$E(4,3,12)$，遇长方体的面反射（反射服从反射原理），将第$i-1$次到第$i$次反射点之间的线段记为$l_i$（$i=2,3,4$），$l_1=AE$，将线段$l_1,l_2,l_3,l_4$竖直放置在同一水平线上，则大致的图形是（        ）

 这个题目用两张图解答：

聪明的你，领悟到其中的玄妙了吗？