一个根式函数值域的问题

求函数\(y=\sqrt{x^2-7x+12}+\sqrt{x^2-3x+2}\)的值域．

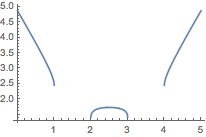显然函数的定义域为\(x\leqslant 1 \lor 2\leqslant x\leqslant 3 \lor x\geqslant 4\)．

先配方，有\[y=\sqrt{\left(x-\dfrac 72\right)^2-\dfrac 14}+\sqrt{\left(x-\dfrac 32\right)^2-\dfrac 14},\]于是不难得出函数关于直线\(x=\dfrac 52\)对称．

换元，令\(t=x-\dfrac 52\)，考虑到对称性，只需要考虑\(0\leqslant t\leqslant \dfrac 12\)以及\(t\geqslant \dfrac 32\)的情形．

求导，得\[y'_t=\dfrac{2t-2}{\sqrt{\left(t-1\right)^2+\dfrac 14}}+\dfrac{2t+2}{\sqrt{\left(t+1\right)^2-\dfrac 14}}.\]

情形一    当\(t\geqslant \dfrac 32\)时，\(y'_t>0\)，于是函数在\(t\geqslant \dfrac 32\)时单调递增，对应的取值范围为\(y\geqslant \sqrt 6\)．

情形二    当\(0\leqslant t\leqslant \dfrac 12\)时，\[\dfrac 12y'_t=\dfrac{1+t}{\sqrt{\left(1+t\right)^2-\dfrac 14}}-\dfrac{1-t}{\sqrt{\left(1-t\right)^2-\dfrac 14},}\]而我们有\[\dfrac{(1-t)^2}{(1+t)^2}\geqslant \dfrac{(1-t)^2-\dfrac 14}{(1+t)^2-\dfrac 14},\]于是可得\(y'_t\leqslant 0\)，等号仅当\(t=0\)时取得．于是函数在\(0\leqslant t\leqslant \dfrac 12\)时单调递减，对应的取值范围为\(\sqrt 2\leqslant y\leqslant \sqrt 3\)．

综上，所求函数的值域为\(\left[\sqrt 2,\sqrt 3\right]\cup\left[\sqrt 6,+\infty\right)\)．

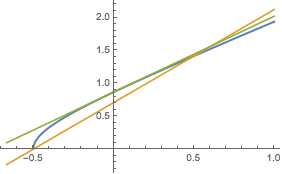
注    （江苏无锡王举老师提供）当\(t\in\left[-\dfrac 12,\dfrac 12\right]\)时也可以利用函数图象的切割线进行放缩，如图．

于是有\[\sqrt 2\cdot t+\dfrac{\sqrt 2}2\leqslant \sqrt{t^2+2t+\dfrac 34}\leqslant \dfrac{2}{\sqrt 3}\cdot t+\dfrac{\sqrt 3}{2},\]类似的，有\[-\sqrt 2\cdot t+\dfrac{\sqrt 2}2\leqslant \sqrt{t^2-2t+\dfrac 34}\leqslant -\dfrac{2}{\sqrt 3}\cdot t+\dfrac{\sqrt 3}{2},\]左边不等式取等号的条件为\(t=\pm\dfrac 12\)，右边不等式取等号的条件为\(t=0\)．因此，有\[\sqrt 2\leqslant y\leqslant \sqrt 3.\]