2014年全国高中数学联赛河北省预赛第5题:
在四面体\(ABCD\)中,\(AB=CD=5\),\(AC=BD=\sqrt{34}\),\(AD=BC=\sqrt{41}\),则\(ABCD\)外接球的表面积是_______.
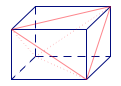
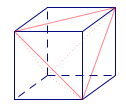
我们知道,任何一个四面体都可以补成一个平行六面体,称这个平行六面体是四面体的外接平行六面体.
特别的,如果四面体的对棱分别相等,那么其外接平行六面体为长方体;如果四面体对棱分别垂直,那么其外接平行六面体的每个面均为菱形;正四面体的外接平行六面体为正方体.
在本题中,易得四面体\(ABCD\)的外接平行六面体为三维分别为\(3\)、\(4\)、\(5\)的长方体,其外接球亦为该长方体的外接球.于是外接球半径\(r\)为长方体对角线长的一半,外接球的表面积为\[4\pi r^2=\pi\cdot\left(3^2+4^2+5^2\right)=50\pi.\]



Pingback引用通告: 每日一题[243] 安全系数 | Math173