每日一题[124] 利用向量转化动点

2015年长沙市一中高考二模文科数学15题：

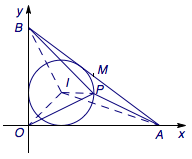
过点$M(4,3)$的动直线$l$交$x$轴的正半轴于点$A$，交$y$轴的正半轴于点$B$．设点$P$是三角形$OAB$的面积取最小值时，三角形$OAB$内切圆上的动点，则$z=PO^2+PA^2+PB^2$的取值范围是_______．

---

正确的答案是$[72,88]$．

这个题的前半段可以参考几何极值的调整法，不难得到$A(8,0)$，$B(0,6)$，三角形$OAB$的内切圆圆心为$I(2,2)$，半径为$2$．

注意到

$$\overrightarrow{PA}=\overrightarrow{PI}+\overrightarrow{IA},$$ 从而有 $$PA^2=PI^2+IA^2+2\overrightarrow{PI}\cdot\overrightarrow{IA},$$ 进而可得 $$\begin{split}\sum{PA^2}&=3PI^2+\sum{IA^2}+2\overrightarrow{PI}\cdot\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IO}\right)\\&=80+2\overrightarrow{PI}\cdot (2,0),\end{split}$$ 于是可得所求的取值范围是$[72,88]$．

---

注    相同的处理技巧（利用向量将动点向定点的方向转化）还可以用来证明三角形的重心到三角形的三个顶点的距离的平方和最小．（提示：先证明$\sum{PA^2}=\sum{GA^2}+3GP^2$．)