每日一题[106]几何极值的调整法

已知直线过点\(M(2,1)\)且与\(x\)、\(y\)轴正半轴分别交于\(A\)、\(B\)两点，\(O\)为坐标原点．求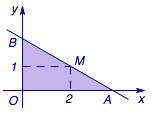： （1）三角形\(AOB\)面积的最小值； （2）三角形\(AOB\)周长的最小值．

三角方法

（1）设\(\angle BAO=x\)，则\[\begin{split}S_{\triangle AOB}&=\dfrac 12OA\cdot OB\\&=\dfrac 12\left(2+\dfrac{1}{\tan x}\right)\left(1+2\tan x\right)\\&=2+2\tan x+\dfrac{1}{2\tan x}\\&\geqslant 4,\end{split}\]等号当且仅当\(\tan x=\dfrac 12\)时取得．

（2）设\(\angle BAO=x\)，则\[c_{\triangle AOB}=3+\dfrac{1}{\sin x}+\dfrac{2}{\cos x}+\dfrac{1}{\tan x}+2\tan x,\]令\(\tan\dfrac{x}{2}=t\)，\(t\in (0,1)\)，则\[\begin{split}c_{\triangle AOB}&=3+\dfrac{1+t^2}{2t}+\dfrac{2\left(1+t^2\right)}{1-t^2}+\dfrac{1-t^2}{2t}+\dfrac{4t}{1-t^2}\\&=1+\dfrac{1}{t}+\dfrac{4}{1-t}\\&\geqslant 10,\end{split}\]这里用到了柯西不等式，取得等号的条件是\(t=\dfrac{1}{3}\)．

代数方法

设直线的横截距和纵截距分别为$\dfrac 1a$和$\dfrac 1b$，则$2a+b=1$($a,b>0$)．

（1）由于$$1=2a+b\geqslant 2\sqrt{2ab},$$于是三角形$AOB$的面积$\dfrac{1}{2ab}$的最小值为$4$．

（2）三角形$AOB$的周长为\[\begin{split} \dfrac 1a+\dfrac 1b+\sqrt{\dfrac 1{a^2}+\dfrac 1{b^2}}&=\dfrac{a+b+\sqrt{a^2+b^2}}{ab}\\&=\dfrac{2}{a+b-\sqrt{a^2+b^2}},\end{split}\]而$$(3a+4b)^2\leqslant 25(a^2+b^2),$$于是$$\sqrt{a^2+b^2}\geqslant \dfrac 35a+\dfrac 45b,$$因此$$a+b-\sqrt{a^2+b^2}\leqslant \dfrac{2a+b}{5}=\dfrac 15,$$从而三角形$AOB$的周长$$\dfrac{2}{a+b-\sqrt{a^2+b^2}}\geqslant 10,$$等号当且仅当$\dfrac{a}{b}=\dfrac 34$时取得．

调整法

（1）如图，设直线在第一象限内的线段被\(M\)平分时与\(x\)轴、\(y\)轴的交点分别为\(P\)、\(Q\)．接下来证明此时三角形\(AOB\)的面积最小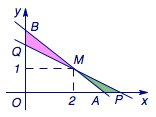． 若不然，假设\(AM<BM\)，则\[\begin{split}S_{\triangle AOB}&=S_{\triangle POQ}-S_{\triangle MAP}+S_{\triangle MBQ}\\&=S_{\triangle POQ}-\dfrac{1}{2} MP\cdot \left(AM-BM\right)\cdot\sin\angle AMP\\&>S_{\triangle POQ},\end{split}\]因此当\(M\)平分\(AB\)时，三角形\(AOB\)的面积最小，最小值为\(4\)．

（2）过\(M\)作圆\(E\)与\(x\)轴、\(y\)轴均相切，作圆\(E\)在\(M\)处的切线，此时三角形\(AOB\)的周长最小，如图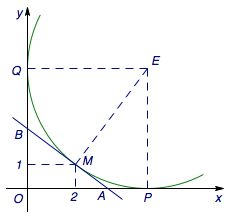． 若不然，\(AB\)为圆\(E\)的割线，此时可以作与该割线平行的切线，则显然有三角形\(AOB\)的周长大于切线与两坐标轴围成的三角形的周长（大小为\(OP+OQ\)），如图． 经计算可得圆\(E:(x-5)^2+(y-5)^2=25\)，\(OP+OQ=10\)，于是三角形\(AOB\)周长的最小值为\(10\)．