已知椭圆$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$($a>b>0$)和直线$l:Ax+By=1$,$P$是直线$l$上一点,射线$OP$交椭圆于点$R$.又点$Q$在射线$OP$上且满足$|OP|\cdot |OQ|=|OR|^2$,当$P$在直线$l$上移动时,求点$Q$的轨迹方程.
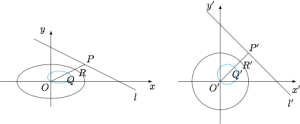
分析与解 如图.
参数方程 设$R(a\cos \theta,b\sin\theta)$,$P\left(pa\cos\theta,pb\sin\theta\right)$,其中$p>0$,则$Q\left(\dfrac 1pa\cos\theta,\dfrac 1pb\sin\theta\right)$.由$P$满足直线$l$的方程,可得\[Apa\cos\theta+Bpb\sin\theta=1,\]而$Q$的参数方程为\[\begin{cases}px=a\cos\theta,\\ py=b\sin\theta,\end{cases}\]可得\[p^2\left(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}\right)=1,\]而\[Ap^2x+Bp^2y=1,\]从而$Q$的轨迹方程为\[Ax+By=\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2},\]即\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}-Ax-By=0,\]其中$x,y$不同时为$0$.
仿射变换 将椭圆$C$仿射变换为$C':x'^2+y'^2=a^2$,则点$Q'$的轨迹是直线$l'$以$O'$为反演中心的圆,其方程为\[\left(\dfrac{x'^2}{a^2}+\dfrac{y'^2}{a^2}-1\right)-\left(Ax'+B\cdot \dfrac bay'-1\right)=0,x^2+y^2\neq 0\]回到原坐标系,其方程为\[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}-Ax-By=0,x^2+y^2\ne 0.\]
事实上,利用相似容易证明$Q'$的轨迹是以$OQ_0'$为直径的圆,其中$Q_0'$是当$OP'\perp l'$时对应的$Q'$位置,如图.而$Q_0'$的坐标容易计算,因此可以方便的推导反演圆方程.