每日一题[760]规划中的换元

已知函数$f(x)=(x^2+ax+b){\rm e}^x$，当$b<1$时，函数$f(x)$在$(-\infty,-2)$和$(1,+\infty)$上均为增函数，则$\dfrac{a+b}{a-2}$的取值范围是_______．

正确答案是$\left(-2,\dfrac 23\right]$．

分析与解    对函数$f(x)$求导得 $$f'(x)=\left[x^2+(a+2)x+(a+b)\right]\cdot{\rm e}^x,$$ 由题意知二次函数$y=x^2+(a+2)x+(a+b)$在$(-\infty,-2)$与$(1,+\infty)$上的函数值非负．

设$m=a-2$，$n=a+b$，则$n-m=b+2<3$，于是问题转化为 $$\forall x\in(-\infty,-2)\cup (1,+\infty),g(x)=x^2+(m+4)x+n\geqslant 0,$$ 求$\dfrac nm$的取值范围．

先考虑此二次函数的判别式 $$\Delta =(m+4)^2-4n>(m+4)^2-4(m+3)=(m+2)^2\geqslant 0,$$ 从而我们得到$(m,n)$的限制条件为 $$\begin{cases} g(-2)=n-2m-4\geqslant 0,\\g(1)=m+n+5\geqslant 0,\\n-m<3,\\-2\leqslant -\dfrac{m+4}2\leqslant 1,\end{cases}$$ 可行域如下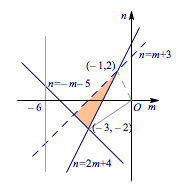：目标函数$\dfrac nm$是可行域中的点$(m,n)$的斜率，求出交点即可得所求范围为$\left(-2,\dfrac 23\right]$．