1．已知数列$\{a_n\}$的通项公式为$a_n=n+\dfrac cn$，若对任意$n\in\mathbf N^*$，都有$a_n\geqslant a_3$，则实数$c$的取值范围是________．
2．证明马青公式：$\dfrac{\pi}4=4\arctan \dfrac 15-\arctan\dfrac{1}{239}$．
3．已知$\alpha,\beta\in\left(-\dfrac{\pi}2,\dfrac{\pi}2\right)$，求证：$\left|\dfrac{\sin^n\alpha+\sin^n\beta}{1+\sin^n\alpha\sin^n\beta}\right|<1$．
4．(2012年浙江卷)已知矩形$ABCD$，$AB=1$，$BC=\sqrt 2$．将$\triangle ABD$沿矩形的对角线$BD$所在的直线进行翻折，在翻折过程中( )
A．存在某个位置，使得直线$AC$与直线$BD$垂直
B．存在某个位置，使得直线$AB$与直线$CD$垂直
C．在某个位置，使得直线$AD$与直线$BC$垂直
D．以上三个命题均不正确
5．到正方体$ABCD-A_1B_1C_1D_1$的三条棱$AB,CC_1,D_1A_1$所在直线的距离都相等的点( )
A．有且仅有$1$个
B．有且仅有$2$个
C．有且仅有$3$个
D．有无数个
6．过点$A(-2,3)$作抛物线$y^2=4x$的两条切线$l_1,l_2$分别与$y$轴交于$B,C$，则$\triangle ABC$的外接圆方程为__________．
7．已知$\forall x\in\mathbf R,ax^3+\dfrac 12x^2+x+1\leqslant {\rm e}^x$，求$a$的值．
参考答案
1．$\left[6,12\right]$．
等价于$a_4\geqslant a_3$且$a_2\geqslant a_3$．
2．由于$\tan 2x=\dfrac{2\tan x}{1-\tan^2x}$，于是$$\tan\left(2\arctan\dfrac 15\right)=\dfrac{\dfrac 25}{1-\dfrac{1}{25}}=\dfrac{5}{12},$$于是$$\tan \left(4\arctan\dfrac 15\right)=\dfrac{\dfrac{5}{6}}{1-\dfrac{25}{144}}=\dfrac{120}{119},$$从而$$\tan\left(4\arctan\dfrac 15-\arctan\dfrac{1}{239}\right)= \dfrac{\dfrac{120}{119}-\dfrac{1}{239}}{1+\dfrac{120}{119}\cdot\dfrac{1}{239}}=1,$$容易知道$4\arctan \dfrac 15-\arctan\dfrac{1}{239}$是一个锐角，因此$$4\arctan \dfrac 15-\arctan\dfrac{1}{239}=\dfrac{\pi}4,$$原命题得证．
注 马青公式是由英国天文学家约翰·马青于1706年发现，他利用这个公式计算得到了圆周率的前100位的值．
3．用分析法，原命题等价于$$\left(\sin^n\alpha+\sin^n\beta\right)^2<\left(1+\sin^n\alpha\sin^n\beta\right)^2,$$即$$\sin^{2n}\alpha+\sin^{2n}\beta+2\sin^n\alpha\sin^n\beta<1+\sin^{2n}\alpha\sin^{2n}\beta+2\sin^n\alpha\sin^n\beta,$$也即$$\left(1-\sin^{2n}\alpha\right)\left(1-\sin^{2n}\beta\right)>0,$$这显然成立．
4．在翻折过程中，$A$点在平面$BCD$上的投影的轨迹为线段$AA'$，如图．
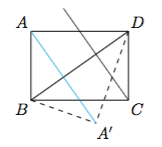根据三垂线定理及其逆定理，空间中的直线垂直可以转化为线影垂直．过$C$作$BD$的垂线$l_1$，过$B$作$CD$的垂线$l_2$，过$D$作$BD$的垂线$l_3$，这三条垂线中只有$l_2$与线段$AA'$有公共点，因此选项B正确．
5．D．
设$P$是对角线$B_1D$所在直线上任意一点，则$\triangle PAB$，$\triangle PCC_1$，$\triangle PD_1A_1$全等，因此$P$到三条棱所在的直线的距离都相等．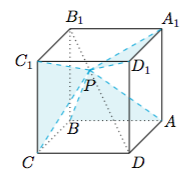
6．$x^2+y^2+x-3y-2=0$．
因为抛物线上一点$M(x_0,y_0)$处的切线方程为$$l:y_0y=2(x+x_0),$$它与$y$轴的交点坐标为$M'\left(0,\dfrac {2x_0}{y_0}\right)$，从而有$$k_l\cdot k_{M'F}=\dfrac 2{y_0}\cdot\dfrac {\frac{2x_0}{y_0}-0}{0-1}=-\dfrac {4x_0}{y_0^2}=-1.$$所以有$FB\perp l_1$，$FC\perp l_2$，于是$AF$是$\triangle ABC$外接圆的直径．
7．$\dfrac 16$．
考虑函数$f(x)={\rm e}^{-x}\cdot\left(ax^3+\dfrac 12x^2+x+1\right)$．求导得$$f'(x)=x^2{\rm e}^{-x}\left(3a-\dfrac 12-ax\right).$$因为$f(0)=1$，而$f(x)\leqslant 1$，所以$0$是$f(x)$的最大值点，也是极大值点，从而有$f'(0)=0$，解得$a=\dfrac 16$．