每日一题[81] 求和的“汉堡包法”

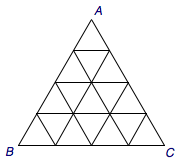
如图，将正三角形$ABC$分割成$n$层共$n^2$个全等的小正三角形，在每个三角形的顶点各放置一个数，使位于同一直线上的点放置的数（当数的个数不少于$3$时）都分别依次成等差数列，若顶点$A$、$B$、$C$处的三个数互不相同且和为$1$，则所有顶点的数之和$S_n=$_______．

---

答案是$\dfrac 16(n+1)(n+2)$．

解题的灵感可以参考http://lanqi.org/?p=177

假设在顶点$A$、$B$、$C$的数分别为$x$、$y$、$z$．考虑将三角形$ABC$旋转$120$度以及$240$度，然后将旋转得到的两个三角形与三角形$ABC$重合放置，那么每个顶点处会有三个数，考虑到等差数列的本质为线性分布，它们分别是

$$\begin{split}\lambda x+\mu y +\nu z,\\\lambda y+\mu z+\nu x,\\\lambda z +\mu x+\nu y,\end{split}$$ 其中$\lambda+\mu+\nu=1$．因此它们的和均为$1$．

于是所有的顶点数除以$3$即为所求：

$$\dfrac 13\left(1+2+\cdots+(n+1)\right)=\dfrac 16(n+1)(n+2).$$