已知单位向量$\overrightarrow a,\overrightarrow b,\overrightarrow c,\overrightarrow x$，且$\overrightarrow a+\overrightarrow b+\overrightarrow c=\overrightarrow 0$，设$y=\Big|\overrightarrow a-\overrightarrow x\Big|+\Big|\overrightarrow b-\overrightarrow x\Big|+\Big|\overrightarrow c-\overrightarrow x\Big|$，则$y$的最大值是______．
分析与解 法一 根据题意，有$\overrightarrow a=-\left(\overrightarrow b+\overrightarrow c\right)$，于是可得$$\overrightarrow a^2=\left(\overrightarrow b+\overrightarrow c\right)^2,$$因此$\overrightarrow b\cdot \overrightarrow c=-\dfrac 12$，类似的，可得$$\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow c=\overrightarrow c\cdot \overrightarrow a=-\dfrac 12.$$因此$\overrightarrow a,\overrightarrow b,\overrightarrow c$是共面向量，且两两的夹角均为$120^\circ$．设$\overrightarrow d$是与$\overrightarrow a,\overrightarrow b,\overrightarrow c$均垂直的单位向量，且$$\overrightarrow x=\lambda \overrightarrow a+\mu \overrightarrow b+\delta \overrightarrow d,$$则$$\overrightarrow x^2=\lambda ^2+\mu^2+\delta^2-\lambda\mu=1.$$此时\[\begin{split} y&=\Big|(\lambda-1)\overrightarrow a+\mu \overrightarrow b+\delta\overrightarrow d\Big|+\Big|\lambda\overrightarrow a+(\mu-1)\overrightarrow b+\delta\overrightarrow d\Big|+\Big|(\lambda+1)\overrightarrow a+(\mu+1)\overrightarrow b+\delta\overrightarrow d\Big|\\
&=\sqrt{(\lambda-1)^2+\mu^2+\delta^2-(\lambda-1)\mu}+\sqrt{\lambda^2+(\mu-1)^2+\delta^2-\lambda(\mu-1)}\\
&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad+\sqrt{(\lambda+1)^2+(\mu+1)^2+\delta^2-(\lambda+1)(\mu+1)}\\
&=\sqrt{2-2\lambda+\mu}+\sqrt{2+\lambda-2\mu}+\sqrt{\lambda+\mu+2}\\
&\leqslant \sqrt 3\cdot \sqrt {(2-2\lambda+\mu)+(2+\lambda-2\mu)+(\lambda+\mu+2)}\\
&=3\sqrt 2,\end{split} \]等号当$\lambda=\mu=0$时取得．因此所求的最大值为$3\sqrt 2$．
法二 由柯西不等式，有\[\begin{split} y&=\Big|\overrightarrow a-\overrightarrow x\Big|+\Big|\overrightarrow b-\overrightarrow x\Big|+\Big|\overrightarrow c-\overrightarrow x\Big|\\
&\leqslant \sqrt 3\cdot \sqrt{\left(\overrightarrow a-\overrightarrow x\right)^2+\left(\overrightarrow b-\overrightarrow x\right)^2+\left(\overrightarrow c-\overrightarrow x\right)^2}\\
&=\sqrt 3\cdot \sqrt{\overrightarrow a^2+\overrightarrow b^2+\overrightarrow c^2+3\overrightarrow x^2-2\overrightarrow x\cdot \left(\overrightarrow a+\overrightarrow b+\overrightarrow c\right)}\\
&=3\sqrt 2
,\end{split} \]等号当$\Big|\overrightarrow a-\overrightarrow x\Big|=\Big|\overrightarrow b-\overrightarrow x\Big|=\Big|\overrightarrow c-\overrightarrow x\Big|$时取得．事实上，有$\overrightarrow a=-\left(\overrightarrow b+\overrightarrow c\right)$，于是可得$$\overrightarrow a^2=\left(\overrightarrow b+\overrightarrow c\right)^2,$$因此$\overrightarrow b\cdot \overrightarrow c=-\dfrac 12$，类似的，可得$$\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow c=\overrightarrow c\cdot \overrightarrow a=-\dfrac 12.$$因此$\overrightarrow a,\overrightarrow b,\overrightarrow c$是共面向量，且两两的夹角均为$120^\circ$．进而取$\overrightarrow x$与$\overrightarrow a,\overrightarrow b,\overrightarrow c$均垂直，即可取得等号．因此所求的最大值为$3\sqrt 2$．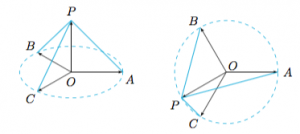
注 如果限定所有向量为平面向量，也可对应的两种方法：
法一 此时$\delta=0$，于是$$\overrightarrow x^2=\lambda^2+\mu^2-\lambda\mu=1,$$且$y=\sqrt{2-2\lambda+\mu}+\sqrt{2+\lambda-2\mu}+\sqrt{\lambda+\mu+2}$．不妨设$\lambda,\mu\geqslant 0$，则不难证明$$\sqrt{2-2\lambda+\mu}+\sqrt{2+\lambda-2\mu}\leqslant 2,\sqrt{\lambda+\mu+2}\leqslant 2,$$等号当$\lambda=\mu=1$时同时取得，因此此时所求的最大值为$4$．
注 事实上，有$$\sqrt{2-2\lambda+\mu}+\sqrt{2+\lambda-2\mu}=\sqrt{\lambda+\mu+2}.$$
法二 设$\overrightarrow a=\overrightarrow {OA}$，$\overrightarrow b=\overrightarrow {OB}$，$\overrightarrow c=\overrightarrow {OC}$，$\overrightarrow x=\overrightarrow {OP}$，且不妨设$P$落在劣弧$BC$上(包括端点)，那么$$y=|PA|+|PB|+|PC|=2|PA|\leqslant 4,$$等号当$PA$为$\triangle ABC$外接圆的直径，即$\overrightarrow x=-\overrightarrow a$时取得．因此所求的最大值为$4$．
注 事实上，有$|PB|+|PC|=|PA|$，由托勒密定理或者平面几何的知识可以证明．