每日一题[641]三角代数式的值域

函数$f(x)=\dfrac{3+5\sin x}{\sqrt{5+4\cos x+3\sin x}}$的值域是______．

---

分析与解　方法一　注意到

$$f(x)=\sqrt{10}\cdot \dfrac{5\sin x+3}{\sqrt{\left(5\sin x+3\right)^2+\left(5\cos x+4\right)^2}},$$ 令$a=5\sin x+3$，$b=5\cos x+4$，则 $$y=\dfrac{5\sin x+3}{\sqrt{\left(5\sin x+3\right)^2+\left(5\cos x+4\right)^2}}$$ 的几何意义是终边过圆$(a-3)^2+(b-4)^2=25$(除去原点)上的点$P(a,b)$的角的余弦(横坐标与到原点距离的比)．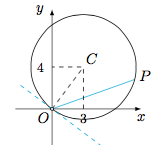
 考虑一个周期内的取值，可得终边过$P$的角的取值范围是$\left(-\arccos\dfrac 45,\pi-\arccos\dfrac 45\right)$，因此余弦值的取值范围是$\left(-\dfrac 45,1\right]$，因此所求函数的值域为$\left(-\dfrac {4\sqrt{10}}5,\sqrt{10}\right]$．

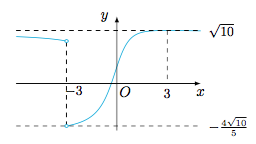
方法二　令$\tan \dfrac x2=t$，则

$$y=\dfrac{3+5\sin x}{\sqrt{5+4\cos x+3\sin x}}=\dfrac{3+5\cdot \dfrac{2t}{1+t^2}}{\sqrt{5+4\cdot\dfrac{1-t^2}{1+t^2}+3\cdot\dfrac{2t}{1+t^2}}}=\dfrac{t+3}{|t+3|}\cdot \dfrac{3t+1}{\sqrt{1+t^2}},$$ 考虑到函数$\varphi(t)=\dfrac{3t+1}{\sqrt{1+t^2}}$的导函数 $$\varphi'(t)=\dfrac{3-t}{(1+t^2)\sqrt{1+t^2}},$$ 于是$\varphi(t)$在$(-3,3)$上单调递增，在$(3,+\infty)$上单调递减．又因为当$t<0$时， $$|\varphi(t)|<\dfrac{|3t|}{\sqrt{1+t^2}}<3,$$ 所以函数$y=\dfrac{t+3}{|t+3|}\cdot \varphi(t)$的图象如图，所求的值域为$\left(-\dfrac {4\sqrt{10}}5,\sqrt{10}\right]$．