利用简单初等函数对$\ln x$($x>1$)进行拟合，并比较各种拟合的精度．
解 列表如下．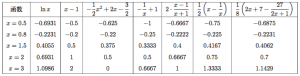
我们定义使得$$\left|\dfrac{\ln x-f(x)}{\ln x}\right|\leqslant \lambda $$的$x$的取值范围中包含$x=1$的区间为$f(x)$的“$\lambda $可信区间”，那么
可以看出一次函数$y=x-1$的“升级版”二次函数$y=-\dfrac 12x^2+2x-\dfrac 32$表现并不好；而反比例函数$y=-\dfrac 1x+1$的“升级版”一次分式函数$y=2\cdot \dfrac{x-1}{x+1}$以及对勾函数$y=2\left(x-\dfrac 1x\right)$的“升级版”对勾函数$y=\dfrac 18\left(2x+7-\dfrac{27}{2x+1}\right)$表现出色．
当然，以上各函数$f(x)$都可以利用换元变为$2f\left(\sqrt x\right)$增加精度，例如利用$$\ln x\approx \dfrac 14\left(2\sqrt x+7-\dfrac{27}{2\sqrt x+1}\right)$$可以估算$\ln 2\approx \dfrac{19-10\sqrt 2}7 = 0.69398\cdots $，这个精度已经非常高了．
我们可以根据具体题目的需要，选择合适的放缩方式．