每日一题[586]二阶不动点的转化

已知$a_{n+1}=\left(\sqrt{a_n}-1\right)^2$，若对任意不小于$2$的正整数$n$均有$a_{n+2}-a_n=0$成立，求$a_1$的取值范围．

分析与解　记$f(x)=\left(\sqrt x-1\right)^2$，则$a_{n+1}=f(a_n)$，于是题意即对任意不小于$2$的正整数$n$均有 $$\begin{cases} a_n=f(a_{n+1}),\\ a_{n+1}=f(a_n),\end{cases}$$ 因此$a_n$是曲线$x=f(y)$与曲线$y=f(x)$的公共点的横坐标．曲线$y=(\sqrt x-1)^2$由曲线$\sqrt x+\sqrt y=1$($0\leqslant x\leqslant 1$)和曲线$\sqrt x-\sqrt y=1$($x>1$)组成，因此问题转化为$a_n\in [0,1]$，其中$n\geqslant 2$且$n\in\mathcal N^*$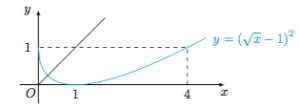．由图易知$a_1=4$是分界点，讨论如下．

情形一　$0\leqslant a_1\leqslant 4$．

此时$a_2\in [0,1]$，而当$x\in [0,1]$时有$f(x)\in [0,1]$，因此$a_n\in [0,1]$，其中$n\geqslant 2$且$n\in\mathbb N^*$，符合题意．

情形二　$a_1>4$．

此时$a_2>1$，不符合题意．

综上所述，$a_1$的取值范围是$[0,4]$．

思考与总结　函数的二阶不动点通常转化为曲线$x=f(y)$与曲线$y=f(x)$的公共点考虑．