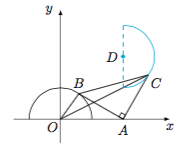
在平面直角坐标系$xOy$中,点$B$为曲线$y=\sqrt{1-x^2}$上的动点,$A(2,0)$,点$C$位于第一象限且$\triangle ABC$为等腰直角三角形,且$A$为直角顶点,则线段$OC$长度的最大值为_______.
分析与解 可以用平面几何的广义托勒密定理或解析几何的轨迹思想解决.
法一 广义托勒密定理
当四边形$OACB$为凸四边形时,如左图: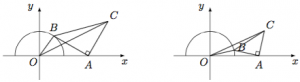 根据广义托勒密定理,有$$OC\cdot AB\leqslant OB\cdot AC+OA\cdot BC=AB+2\sqrt 2AB,$$于是$OC\leqslant 1+2\sqrt 2$,等号当$O,A,C,B$四点共圆时取得(此时$\angle BOA=135^\circ$),所以在这种情况下$OC$的最大值为$1+2\sqrt 2$.
根据广义托勒密定理,有$$OC\cdot AB\leqslant OB\cdot AC+OA\cdot BC=AB+2\sqrt 2AB,$$于是$OC\leqslant 1+2\sqrt 2$,等号当$O,A,C,B$四点共圆时取得(此时$\angle BOA=135^\circ$),所以在这种情况下$OC$的最大值为$1+2\sqrt 2$.
当四边形$OACB$不是凸四边形时,如右图.有$$OC\leqslant OB+BC=OB+{\sqrt 2}AC<OB+\sqrt 2{OA}=1+2\sqrt 2.$$法二 轨迹
如图,点$C$运动的轨迹是以$D(2,2)$为圆心的半圆弧(考虑$\triangle OAB$绕$A$点顺时针旋转$90^\circ$得到$\triangle DAC$即可),于是$OC$的最大值为$1+2\sqrt 2$.