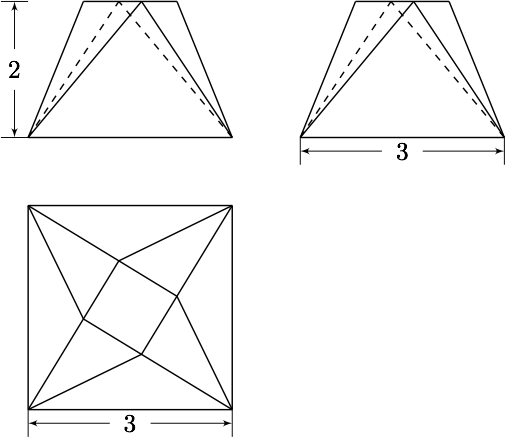
一个多面体的三视图如图所示,其中俯视图中内部的小正方形边长为$1$,求该多面体的体积.
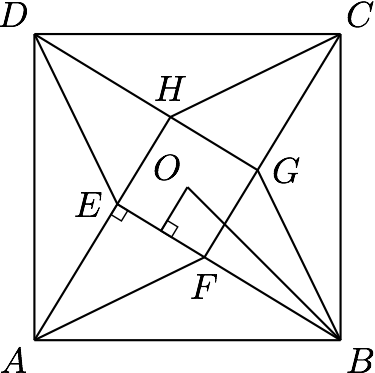
分析与解 根据题意,该多面体的直观图如图所示为$EFGH-ABCD$.
为了方便计算体积,我们计算它的四分之一$PFG-OBC$,其中$O,P$分别为下底面和上底面的中心,如图.
根据题意,有\[\begin{split}V_{ PFG-OBC}&=V_{O-PFG}+V_{FG-OB}+V_{G-OBC}\\ &= \dfrac 13\cdot S_{\triangle PFG}\cdot OP+\dfrac 16\cdot FG\cdot OB\cdot OP\cdot \sin<FG,OB>+\dfrac 13\cdot S_{\triangle OBC}\cdot OP.\end{split}\]
如图,设$AE=BF=x$,则在直角三角形$ABE$中,有$$x^2+(1+x)^2=9,$$解得$$x=\dfrac{\sqrt{17}-1}2,$$于是$$OB\cdot \sin <FG,OB>= \dfrac{\sqrt{17}}2,$$因此$$V_{ PFG-OBC}=\dfrac 53+\dfrac{\sqrt{17}}6,$$进而可得$$V_{EFGH-ABCD}=4V_{PFG-OBC}=\dfrac{20}3+\dfrac {2\sqrt {17}}3.$$
注 由异面线段$AB,CD$组成的四面体的体积$$V_{AB-CD}=\dfrac 16\cdot AB\cdot CD\cdot d(AB,CD)\cdot \sin <AB,CD>,$$其中$d(AB,CD)$为$AB,CD$所在的直线间的距离,而$<AB,CD>$指$AB,CD$所在的直线的夹角.这个公式在计算用对边描述的四面体的体积时非常有用.




get it
我认为我的方法更简单一些。
在“分析与解”的第一幅图中,设E在平面ABCD上的射影为I。
考虑四棱锥A-EFBI的体积。很容易计算。
几何体EFGH-ABCD可被分割为四个上述四棱锥和中间的长方体。
得到的答案与“分析与解”中的答案相同。
是的.放这个题的本意是想讲一下对棱扭成的四面体体积的计算方式.