数形结合需谨慎

下面这道题目是2013年高考天津卷理科数学第7题：

函数$f(x)=2^x\left|{\log_{0.5}}x\right|-1$的零点个数为（        ）

A．$1$

B．$2$

C．$3$

D．$4$

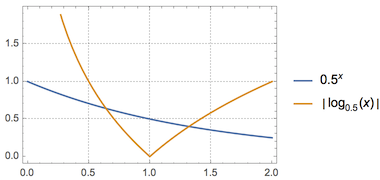
错解    函数$f(x)$的零点可以看成是函数$y=\left|{\log_{0.5}}x\right|$和函数$y=0.5^x$的图象的公共点的横坐标，如图．

根据图象，可得所求函数的零点个数为$2$，选B．

分析    根据函数的图象，可以确定当$x\geqslant 1$时，两个函数必然有且只有一个公共点；但是在区间$(0,1)$上，我们并没有足够的证明说明两个函数只有一个公共点（有公共点是必然的，因为两个函数在$x\to 0$和$x\to 1$时相对位置发生了颠倒．

改正    当$0<x<1$时，考虑函数$g(x)=2^x\ln x+\ln 2$，其导函数$$g'(x)=\dfrac{2^x}{x}\cdot (1+x\ln x\cdot \ln 2),$$而$$1+x\ln x\cdot \ln 2>1-\dfrac{\ln 2}{\rm e}>0,$$于是$g(x)$单调递增，而当$x\to 0$时，$g(x)\to -\infty$；$g(1)=\ln 2>0$，因此函数$g(x)$在区间$(0,1)$上有唯一零点．

探究一   是不是当$0<a<1$时，函数$y={\log_a}x$和函数$y=a^x$在区间$(0,1)$上一定有唯一公共点呢？

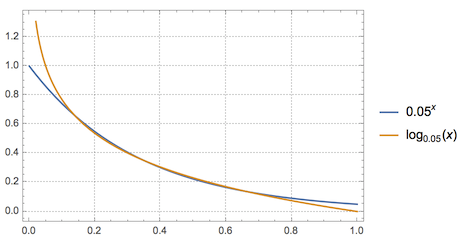
答案是否定的，利用Mathematica，我们可以知道，当$a=0.05$时，这两个函数在区间$(0,1)$上有三个公共点，如图．

那么，这两个函数在区间$(0,1)$上的公共点个数是否还有其他可能？影响公共点个数的参数$a$的分界点又是多少呢？

探究二    设$m=\dfrac 1a$，考虑函数$h(x)=m^x\ln x+\ln m$，则其导函数$$h'(x)=\dfrac{m^x}{x}\cdot (1+x\ln x\cdot \ln m),$$于是当$\ln m\leqslant {\rm e}$，即$a\geqslant {\rm e}^{-\rm e}$时，$h'(x)\geqslant 0$，于是$h(x)$单调递增，所求的公共点个数为$1$．

当$\ln m>{\rm e}$，即$0<a<{\rm e}^{-{\rm e}}$时，函数$h'(x)$在$(0,1)$上有两个零点，设为$x_1,x_2$，且$0<x_1<\dfrac{1}{\rm e}<x_2<1$，则函数$h(x)$在$(0,x_1)$上单调递增，在$(x_1,x_2)$上单调递减，在$(x_2,1)$上单调递增．

考虑到$x_1,x_2$是关于$x$的方程$$x\ln x\cdot \ln m+1=0$$的两个解，所以$$\ln m=-\dfrac{1}{x_1\ln x_1}=-\dfrac {1}{x_2\ln x_2},$$于是极值$$h(t)={\rm e}^{-\frac{1}{\ln t}}\cdot \ln t-\dfrac{1}{t\ln t},$$其中$t=x_1$或$t=x_2$．令$-\dfrac{1}{\ln t}=x$知考虑函数$$\varphi (x)={\rm e}^{\frac 1x}\cdot x-{\rm e}^x\cdot \dfrac 1x.$$即可．利用极值点偏移，我们很容易证明当$x<1$时，$\varphi(x)>0$；当$x>1$时，$\varphi(x)<0$；因此可得函数$h(x)$的极大值$h(x_1)>0$，极小值$h(x_2)<0$，因此函数$h(x)$在区间$(0,x_1)$，$(x_1,x_2)$，$(x_2,1)$上各有一个零点，所求的公共点个数为$3$．

总结    若将题目改成

函数$f(x)=\dfrac{1}{a^x}\left|{\log_a}x\right|-1$($0<a<1$)的零点个数为_______．

则答案应该是$\begin{cases} 2,a\geqslant {\rm e}^{-{\rm e}},\\4,0<a<{\rm e}^{-{\rm e}}.\end{cases} $