每日一题[66] 向量螺旋

已知$\overrightarrow a$，$\overrightarrow b$是非零向量，构造集合 $$P=\left\{\overrightarrow p\left|\overrightarrow p=t\overrightarrow a+\overrightarrow b,t\in\mathcal R\right.\right\}.$$ 记$P$中模最小的向量为$T\left(\overrightarrow a,\overrightarrow b\right)$．

（1）对于$T\left(\overrightarrow a,\overrightarrow b\right)=t\overrightarrow a+\overrightarrow b$，求$t$的值．（用$\overrightarrow a$，$\overrightarrow b$来表示）

（2）证明：$T\left(\overrightarrow a,\overrightarrow b\right)\perp \overrightarrow a$；

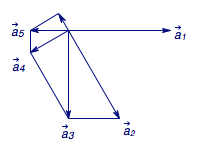
（3）若$\left|\overrightarrow a_1\right|=\left|\overrightarrow a_2\right|=1$且$\langle \overrightarrow a_1,\overrightarrow a_2\rangle=\dfrac{\pi}3$．构造向量序列$\overrightarrow{a_n}=T\left(\overrightarrow a_{n-2},\overrightarrow a_{n-1}\right)$，其中$n\in\mathcal N^*$，$n\geqslant 3$．请直接写出$\left|\overrightarrow{a_n}\right|$的值．

（1）由于 $$\left|T\left(\overrightarrow a,\overrightarrow b\right)\right|^2=\left(\overrightarrow a\cdot \overrightarrow a\right)t^2+\left(2\overrightarrow a\cdot \overrightarrow b\right)t+\left(\overrightarrow b\cdot \overrightarrow b\right),$$ 于是 $$t=-\dfrac{\overrightarrow a\cdot\overrightarrow b}{\overrightarrow a\cdot\overrightarrow a}.$$

（2）根据（1）的结果，有 $$T\left(\overrightarrow a,\overrightarrow b\right)\cdot\overrightarrow a=t\overrightarrow a\cdot\overrightarrow a+\overrightarrow a\cdot\overrightarrow b=0,$$ 因此原命题成立．

（3）如图可得 $$\left|\overrightarrow a_n\right|=\begin{cases}1,&n=1,\\\left(\dfrac{\sqrt 3}4\right)^{\frac n2-1},&n\geqslant 2\land n\mid 2\\2\left(\dfrac{\sqrt 3}4\right)^{\frac{n-1}2}&n\geqslant 3\land n\nmid 2.\end{cases}$$