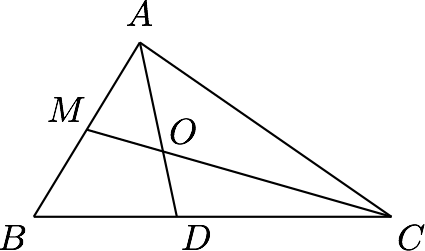
在$\triangle ABC$中,$AB=2$,$AC=3$,角$A$的平分线$AD$与$AB$边上的中线$CM$的交点为$O$,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$,则$x+y=$_______.
法一
根据向量分解的系数和与比的几何意义可得$$x+y=\dfrac{AO}{AD},\dfrac xy=\dfrac{CD}{BD}.$$
由角平分线定理可得$$\dfrac xy=\dfrac{CD}{BD}=\dfrac 32,$$进而对$\triangle ABD$和截线$MCO$应用梅涅劳斯定理可得$$\dfrac{AM}{MB}\cdot\dfrac{BC}{CD}\cdot\dfrac{DO}{OA}=1,$$于是$\dfrac{DO}{OA}=\dfrac 35$,因此$x+y=\dfrac 58$.
法二
由角平分线定理可得$\dfrac{MO}{OC}=\dfrac 13$,于是$$\overrightarrow{AO}=\dfrac 34\overrightarrow{AM}+\dfrac 14\overrightarrow{AC}=\dfrac 38\overrightarrow{AB}+\dfrac 14\overrightarrow{AC},$$因此$x+y=\dfrac 58$.


请问$x+y$和$x/y$的几何意义怎么来的?
和是根据向量共线的表达,商是根据角平分线定理