已知函数$f(x)=x|x-a|$($a>0$).
(1)不等式$f(x)\leqslant 1$在$[0,m]$上恒成立,当$m$取得最大值时,求$a$的值;
(2)在(1)的条件下,若对于任意$x\in\mathcal R$,不等式$f(x+t)\geqslant f(x)-t$($t>0$)恒成立,求$t$的取值范围.
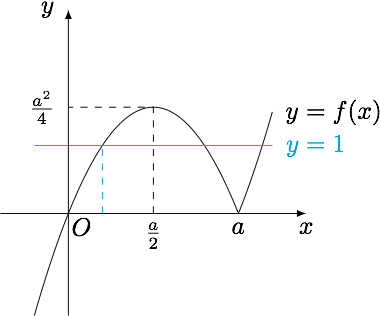
解 (1)函数$f(x)$的图象如图所示,“拱形”的高度为$\dfrac{a^2}4$.
当$\dfrac{a^2}{4}>1$时,直线$y=1$穿过“拱形”,于是$m$的最大值为方程$$-x^2+ax=1$$的较小根,为$\dfrac{a-\sqrt{a^2-4}}2$,显然有$$\dfrac{a-\sqrt{a^2-4}}2=\dfrac{2}{a+\sqrt{a^2-4}}<1;$$
当$\dfrac{a^2}{4}\leqslant 1$时,直线$y=1$不穿过“拱形”,于是$m$的最大值为方程$$x^2-ax=1$$的较大根,为$\dfrac{a+\sqrt{a^2+4}}2$,有$$\dfrac{a+\sqrt{a^2+4}}2\leqslant 1+\sqrt 2,$$当$a=2$时取得等号.
综上所述,当$a=2$时,$m$取得最大值$1+\sqrt 2$.
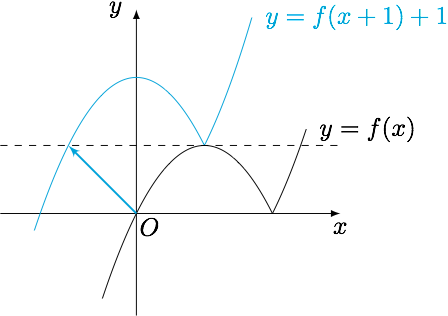
(2)相当于将$y=f(x)$的图象沿向量$(-t,t)$平移后得到的图象在原函数图象上方.问题的关键还是在使得“拱形”安全撤离上.
“拱形”的左侧只要稍加平移就能满足条件,因此核心困难在于“拱形”的右侧,单独考虑$x=2-t$处,此时有$$f(2)\geqslant f(2-t)-t,$$即$$0\geqslant t(2-t)-t,$$解得$t\geqslant 1$.
事实上,当$t=1$时,画出函数图象可知“拱形”已经安全撤离.因此接下来我们证明当$t\geqslant 1$时,题中不等式恒成立.
当$x<0$或$x>2$时,由于函数$f(x)$单调递增.
于是当$x>2$或$\begin{cases} x<0,\\x+t\leqslant 0\end{cases} $时,有$f(x+t)>f(x)$;
当$\begin{cases} x<0,\\x+t>0\end{cases} $时,有$f(x+t)>0>f(x)$;
综上知,$$f(x+t)>f(x)>f(x)-t,$$不等式成立;
当$0\leqslant x\leqslant 2$时,有$$f(x+t)+t\geqslant 1\geqslant f(x),$$不等式成立.
综上所述,$t$的取值范围是$[1,+\infty)$.