2012年高考数学江苏卷第14题(填空压轴题):
已知正数$a,b,c$满足:$5c-3a\leqslant b\leqslant 4c-a$,$c\ln b\geqslant a+c\ln c$,则$\dfrac ba$的取值范围是_____.
正确答案是$[\mathrm e,7]$.
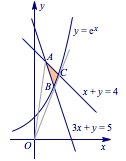
解 题目条件中的不等式含有三个参数,其中不等式$5c-3a\leqslant b\leqslant 4c-a$为齐次式,而不等式$c\ln b\geqslant a+c\ln c$可以转化成$\ln\dfrac bc\geqslant \dfrac ac$,于是我们令$x=\dfrac ac,y=\dfrac bc$,将条件转化为\[\begin{cases} x+y\leqslant 4,\\3x+y\geqslant 5,\\y\geqslant {\mathrm e}^x.\end{cases} \]它表示的平面区域如下图:
因为目标函数$\dfrac ba=\dfrac yx$为可行域中一点与原点连线的斜率,所以点$A\left(\dfrac 12,\dfrac 72\right )$对应目标函数的最大值$7$.
下面考虑目标函数的最小值:
容易求出过原点且与$y=\mathrm{e}^x$相切的直线为$y=\mathrm{e}x$,切点坐标为$M(1,\mathrm{e})$,而点$M$在可行域内,且有$\mathrm e^x\geqslant \mathrm {e}x$,故$\dfrac yx$的最小值为$\mathrm e$.从而知所求的取值范围为$[\mathrm e,7]$.
多参数问题具有某种对称性时,常考虑用换元法将题目的条件与结论转化成更容易处理的形式,更多类似问题见每日一题[324]移花接木.