每日一题[54] 强势放缩

已知数列\(\left\{a_n\right\}\)满足\(a_1=1\)，\(a_{n+1}=a_n+\dfrac{1}{a_n}\)，求证：\(a_{2015}>63\)．

 首先由初值\(a_1=1\)，以及迭代函数\(y=x+\dfrac{1}{x}\)的图象可得数列\(\left\{a_n\right\}\)发散．

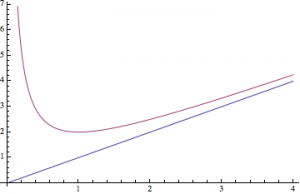考虑作差\[a_{n+1}-a_n=\dfrac{1}{a_n},\]然而得到的结果是趋于\(0\)的，这使得我们无法依此去估计\(a_{2015}\)的取值下界．

因此，可以尝试放大\(a_{n+1}\)与\(a_n\)的距离．当然，按比例放大是不行的（比如说两边同时乘以\(10\)是无效的．事实上，方幂可以有效的将微小的差距扩大，因此两边平方有\[a_{n+1}^2=a_n^2+2+\frac{1}{a_n^2},\]于是可得\[a_{n+1}^2-a_n^2>2,\]进而有\[a_{2015}^2>2\times 2014+a_1^2=4029,\]两边开方就能推得欲证结论．

当然，我们也可以将两边立方，但这样会“浪费”很多，最后得到的结果反而不如平方好了．

最后给一个补充练习：

已知数列\(\left\{a_n\right\}\)满足\(a_1=1\)，\(a_{n+1}=a_n+\dfrac{1}{a_n^2}\)，求证：\(a_{2015}>18\)．