2015年全国高中数学联合竞赛A卷

一试

一、填空题 本小题共8小题，每小题8分，满分64分．

1、设\(a,b\)是不相等的实数，若二次函数\(f(x)=x^2+ax+b\)满足\(f(a)=f(b)\)，则\(f(2)\)的值为_______． 2、若实数\(\alpha\)满足\(\cos\alpha=\tan\alpha\)，则\(\dfrac{1}{\sin\alpha}+\cos^4\alpha\)的值为_______．

3、已知复数数列\(\left\{z_n\right\}\)满足\(z_1=1\)，\(z_{n+1}=\overline{z_n}+1+n{\rm i}\)，其中\(n=1,2,\cdots\)，其中\(\rm i\)是虚数单位，\(\overline{z_n}\)表示\(z_n\)的共轭复数，则\(z_{2015}\)的值为_______．

4、在矩形\(ABCD\)中，\(AB=2\)，\(AD=1\)，在\(DC\)边上（包含点\(D\)、\(C\)）的动点\(P\)与\(CB\)延长线上（包含\(B\)）的动点\(Q\)满足\(\left|\overrightarrow{DP}\right|=\left|\overrightarrow{BQ}\right|\)，则向量\(\overrightarrow{PA}\)与向量\(\overrightarrow{PQ}\)的数量积\(\overrightarrow{PA}\cdot\overrightarrow{PQ}\)的最小值为_______．

5、在正方体中随机取\(3\)条棱，它们两两异面的概率为________．

6、在平面直角坐标系\(xOy\)中，点集\[K=\left\{(x,y)\left|\left(|x|+|3y|-6\right)\left(|3x|+|y|-6\right)\leqslant 0\right.\right\}\]所对应的平面区域的面积为_______．

7、设\(\omega\)为正实数，若存在\(a,b\)（\(\pi\leqslant a<b\leqslant 2\pi\)），使得\(\sin\omega a+\sin\omega b=2\)，则\(\omega\)的取值范围是_______．

8、对四位数\(\overline{abcd}\)（\(1\leqslant a\leqslant 9\)，\(0\leqslant b,c,d\leqslant 9\)），若\(a>b\)，\(b<c\)，\(c>d\)，则称\(\overline{abcd}\)为\(P\)类数，若\(a<b\)，\(b>c\)，\(c<d\)，则称\(\overline{abcd}\)为\(Q\)类数．用\(N(P)\)与\(N(P)\)分别表示\(P\)类数与\(Q\)类数的个数，则\(N(P)-N(Q)\)的值为_______．

二、解答题 本大题共3小题，满分\(56\)分，解答应写出文字说明、证明过程或演算步骤．

9、（本小题满分16分）若实数\(a,b,c\)满足\(2^a+4^b=2^c\)，\(4^a+2^b=4^c\)，求\(c\)的最小值．

10、（本小题满分20分）设\(a_1,a_2,a_3,a_4\)是\(4\)个有理数，使得\[\left\{a_ia_j\left|1\leqslant i< j\leqslant 4\right.\right\}=\left\{-24,-2,-\dfrac 32,-\dfrac 18,1,3\right\},\]求\(a_1+a_2+a_3+a_4\)的值．

11、（本小题满分20分）在平面直角坐标系\(xOy\)中，\(F_1\)、\(F_2\)分别是椭圆\(\dfrac{x^2}{2}+y^2=1\)的左、右焦点，设不经过焦点\(F_1\)的直线\(l\)与椭圆交于两个不同的点\(A\)、\(B\)，焦点\(F_2\)到直线\(l\)的距离为\(d\)．如果直线\(AF_1\)、\(l\)、\(BF_1\)的斜率依次成等差数列，求\(d\)的取值范围．

加试

一、（本题满分40分）设\(a_1,a_2,\cdots,a_n\)（\(n\geqslant 2\)）是实数，证明：可以选取\(\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n\in\left\{-1,1\right\}\)，使得\[\left(\sum_{i=1}^n{a_i}\right)^2+\left(\sum_{i=1}^n{\varepsilon_ia_i}\right)^2\leqslant (n+1)\left(\sum_{i=1}^na_i^2\right).\]

二、（本题满分40分）设\(S=\left\{A_1,A_2,\cdots,A_n\right\}\)，其中\(A_1,A_2,\cdots,A_n\)是\(n\)个互不相同的有限集合（\(n\geqslant 2\)），满足对任意\(A_i,A_j\in S\)，均有\(A_i\cup A_j\in S\)．若\(k=\min\limits_{1\leqslant i\leqslant n}\left|A_i\right|\geqslant 2\)．证明：存在\(x\in\bigcup\limits_{i=1}^n{A_i}\)，使得\(x\)属于\(A_1,A_2,\cdots,A_n\)中的至少\(\dfrac nk\)个集合（这里\(|X|\)表示有限集合\(X\)的元素个数）.

三、（本题满分50分）如图，\(\triangle ABC\)内接于圆\(O\)，\(P\)为弧\(BC\)上一点，点\(K\)在线段\(AP\)上，使得\(BK\)平分\(\angle ABC\)．过\(K\)、\(P\)、\(C\)三点的圆\(\Omega\)与边\(AC\)交于点\(D\)，连接\(BD\)交圆\(\Omega\)于点\(E\)，连接\(PE\)并延长与边\(AB\)交于点\(F\)，证明：\(\angle ABC=2\angle FCB\)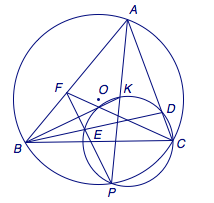．四、求具有下列性质的所有正整数\(k\)：对任意正整数\(n\)，\(2^{(k-1)n+1}\)不整除\(\dfrac{(kn)!}{n!}\)．

---

参考答案

以下解析抄录自《学数学》编辑部发布的《2015年全国高中数学联赛（A卷）参考答案及评分标准》，有部分删节和修改．

一试

一、填空题

1、\(4\)

提示    \(x=\dfrac{a+b}2\)是\(f(x)\)的对称轴，于是可得\(2a+b=0\)．

2、\(2\)

提示    \(\sin^2\alpha+\sin\alpha=1\)，于是\[\dfrac{1}{\sin\alpha}+\cos^4\alpha=\sin\alpha+1+\sin^2\alpha=2.\]

3、\(2015+1007{\rm i}\)

提示    \(z_{n+2}=z_n+2+{\rm i}\)．

4、\(\dfrac 34\)

提示    建系即可．

5、\(\dfrac {2}{55}\)

提示    将正方体的\(12\)条棱按方向分为\(3\)组．

6、\(24\)

提示    考虑到对称性，先处理第一象限的情形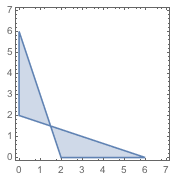． 然后再乘\(4\)即可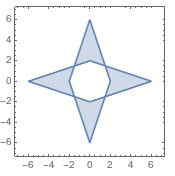． 7、\(\left[\dfrac 94,\dfrac 52\right]\cup\left[\dfrac{13}4,+\infty\right)\)

提示    \(\omega a\)和\(\omega b\)必然形如\(2k\pi+\dfrac{\pi}2\)，讨论即得．

8、\(285\)

提示    所求即所有以\(0\)结尾的\(P\)类数．

二、解答题

9、记\(x=2^a\)，\(y=2^b\)，\(z=2^c\)，则\[\begin{cases}x+y^2=z,\\x^2+y=z^2,\end{cases}\]消元得\[\left(z-y^2\right)^2+y=z^2,\]整理得\[\begin{split}z&=\dfrac{y^2}{2}+\dfrac{1}{2y}\\&=\dfrac{y^2}2+\dfrac{1}{4y}+\dfrac{1}{4y}\\&\geqslant 3\sqrt[3]{\dfrac{y^2}2\cdot\dfrac{1}{4y}\cdot\dfrac{1}{4y}}\\&=\dfrac{3}{4}\sqrt[3]{2},\end{split}\]等号当\(y=\dfrac{1}{\sqrt[3]2}\)，\(x=\dfrac{\sqrt[3]2}4\)时取得． 于是\(z\)的最小值为\(\dfrac{3}4\sqrt[3]2\)，进而\(c\)的最小值为\({\log_2}\left(\dfrac 34\sqrt[3]2\right)={\log_2}3-\dfrac 53\)．

10、设\(a_1,a_2,a_3,a_4\)的绝对值从小到大排列，则\[\begin{cases}a_1a_2=-\dfrac 18,\\a_1a_3=1,\\a_2a_4=3,\\a_3a_4=-24,\\\left\{a_2a_3,a_1a_4\right\}=\left\{-2,-\dfrac 32\right\},\end{cases}\]解得\[\left(a_1,a_2,a_3,a_4\right)=\left(\dfrac 14,-\dfrac 12,4,-6\right)\lor\left(-\dfrac 14,\dfrac 12,-4,6\right),\]于是\(a_1+a_2+a_3+a_4=\pm\dfrac 94\)．

11、根据已知，有\(F_1(-1,0)\)，\(F_2(1,0)\)．设\(l:y=kx+m\)，\(A\left(x_1,y_1\right)\)，\(B\left(x_2,y_2\right)\)，则联立直线与椭圆方程得\[\begin{eqnarray}\left(2k^2+1\right)x^2+4kmx+2m^2-2=0,\end{eqnarray}\]判别式\[\Delta=8\left(2k^2+1-m^2\right)>0,\]即\[\begin{eqnarray}2k^2+1>m^2.\end{eqnarray}\] 由题意直线\(AF_1\)、\(l\)、\(BF_1\)的斜率成等差数列，得\[\dfrac{y_1}{x_1+1}+\dfrac{y_2}{x_2+1}=2k,\]将\(y_1=kx_1+m\)，\(y_2=kx_2+m\)代入并整理得\[(m-k)\left(x_1+x_2+2\right)=0,\]由直线\(l\)不经过\(F_1\)点，舍去\(m-k=0\)，于是\[x_1+x_2=-2,\]结合(1)的韦达定理有\[-\dfrac{4km}{2k^2+1}=-2,\]即\[\begin{eqnarray}m=k+\dfrac 1{2k}.\end{eqnarray}\] 由(2)(3)可得\(k^2\)的取值范围由\[2k^2+1>m^2=\left(k+\dfrac{1}{2k}\right)^2\]确定，即\[k^2>\dfrac 12.\] 点\(F_2(1,0)\)到直线\(l\)的距离为\[d=\dfrac{|k+m|}{\sqrt{1+k^2}}=\sqrt{\dfrac{k^2}{1+k^2}}\cdot\left(2+\dfrac{1}{2k^2}\right),\]结合\(k^2\)的取值范围可得\(d\)的取值范围为\(\left(\sqrt 3,2\right)\)．

加试

一、（本题满分40分）

证法一

我们证明\[\begin{eqnarray}\left(\sum_{i=1}^na_i\right)^2+\left(\sum_{i=1}^ma_i-\sum_{i=m+1}^na_i\right)^2\leqslant (n+1)\left(\sum_{i=1}^na_i^2\right),\end{eqnarray}\]其中\(m=\left[\dfrac n2\right]\)，即\[\varepsilon_i=\begin{cases}1,&i=1,2,\cdots,m,\\-1,&i=m+1,m+2,\cdots,n.\end{cases}\] 事实上，(4)的左边为\[\begin{split}&\quad\left(\sum_{i=1}^ma_i+\sum_{j=m+1}^na_j\right)^2+\left(\sum_{i=1}^ma_i-\sum_{j=m+1}^na_j\right)^2\\&=2\left(\sum_{i=1}^ma_i\right)^2+2\left(\sum_{j=m+1}^na_j\right)^2\\&\leqslant 2m\sum_{i=1}^ma_i^2+2(n-m)\sum_{j=m+1}^na_j^2\\&=2\left[\dfrac n2\right]\sum_{i=1}^ma_i^2+2\left[\dfrac{n+1}2\right]\sum_{j=m+1}^na_j^2\\&\leqslant n\sum_{i=1}^ma_i^2+(n+1)\sum_{j=m+1}^na_j^2\\&\leqslant (n+1)\sum_{i=1}^na_i^2,\end{split}\]其中第三行用到了柯西不等式． 从而(4)得证，原题得证．

证法二

首先，由于问题中\(a_1,a_2,\cdots,a_n\)的对称性，可设\(a_1\geqslant a_2\geqslant \cdots \geqslant a_n\)，此外，若将\(a_1,a_2,\cdots,a_n\)中的负数均改变符号，则问题中的不等式左边的\(\left(\sum\limits_{i=1}^na_i\right)^2\)不减，而右边的\(\sum\limits_{i=1}^na_i^2\)不变，并且此变化不影响\(\varepsilon\)的选取，因此我们可以进一步设\(a_1\geqslant a_2\geqslant \cdots a_n\geqslant 0\)．

引理    设\(a_1\geqslant a_2\geqslant \cdots a_n\geqslant n\)，则\[0\leqslant \sum_{i=1}^n\left(-1\right)^{i-1}a_i\leqslant a_1.\] 引理的证明从略． 于是回到原题，由柯西不等式及上述引理可得\[\begin{split}\left(\sum_{i=1}^na_i\right)^2+\left(\sum_{i=1}^n(-1)^{i-1}a_i\right)^2&\leqslant n\sum_{i=1}^na_i^2+a_1^2\\&\leqslant (n+1)\sum_{i=1}^na_i^2,\end{split}\]这就证明了结论．

二、（本题满分40分） 不妨设\(\left|A_1\right|=k\)．设在\(A_1,A_2,\cdots,A_n\)中与\(A_1\)不相交的集合有\(s\)个，重新记为\(B_1,B_2,\cdots,B_s\)，设包含\(A_1\)的集合有\(t\)个，重新记为\(C_1,C_2,\cdots,C_t\)．由已知条件\(\left(B_i\cup A_1\right)\in S\)，即\[\left(B_i\cup A_1\right)\in\left\{C_1,C_2,\cdots,C_t\right\},\]这样我们得到一个映射\[f:\left\{B_1,B_2,\cdots,B_s\right\}\to\left\{C_1,C_2,\cdots,C_t\right\},f\left(B_i\right)=B_i\cup A_1,\]显然\(f\)是单射，于是\(s\leqslant t\)． 设\(A_1=\left\{a_1,a_2,\cdots,a_k\right\}\)．在\(A_1,A_2,\cdots,A_n\)中除去\(B_1,B_2,\cdots,B_s,C_1,C_2,\cdots,C_t\)后在剩下的\(n-s-t\)个集合中，设包含\(a_i\)的集合有\(x_i\)个（\(1\leqslant i\leqslant k\)），由于剩下的\(n-s-t\)个集合中每个集合与\(A_1\)的交集非空，即包含某个\(a_i\)，从而\[x_1+x_2+\cdots+x_k\geqslant n-s-t.\] 不妨设\(x_1=\max\left\{x_1,x_2,\cdots,x_k\right\}\)，则由上式知\[x_1\geqslant \dfrac{n-s-t}k,\]即在剩下的\(n-s-t\)个集合中，包含\(a_1\)的集合至少有\(\dfrac{n-s-t}k\)个．又由于\(A_1\subseteq C_i\)（\(i=1,2,\cdots,t\)），故\(C_1,C_2,\cdots,C_t\)都包含\(a_1\)，因此包含\(a_1\)的集合个数至少为\[\begin{split}\dfrac{n-s-t}k+t&=\dfrac{n-s+t(k-1)}k\\&\geqslant \dfrac{n-s+t}k\\&\geqslant \dfrac nk.\end{split}\]

三、（本题满分50分） 设\(CF\)与圆\(\Omega\)交于点\(L\)（异于\(C\)）．

证法一

连接\(PB\)、\(PC\)、\(BL\)、\(KL\)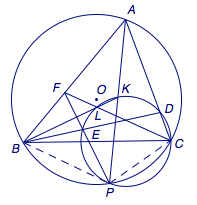． 注意此时\(C\)、\(D\)、\(L\)、\(K\)、\(E\)、\(P\)六点均在圆\(\Omega\)上，结合\(A\)、\(B\)、\(P\)、\(C\)四点共圆，可知\[\angle FEB=\angle DEP=180^\circ-\angle DCP=\angle ABP=\angle FBP,\]因此\(\triangle FBE\sim\triangle FPB\)，因此\[FB^2=FE\cdot FP.\] 又由圆幂定理可知，\(FE\cdot FP=FL\cdot FC\)，所以\[FB^2=FL\cdot FC,\]因此\(\triangle FBL\sim\triangle FCB\)． 因此\[\angle FLB=\angle FBC=\angle APC=\angle KPC=\angle FLC,\]即\(B\)、\(K\)、\(L\)三点共线． 再根据\(\triangle FBL\sim\triangle FCB\)得\[\angle FCB=\angle FBL=\angle FBE=\dfrac 12\angle ABC,\]即\(\angle ABC=2\angle FCB\)．

证法二 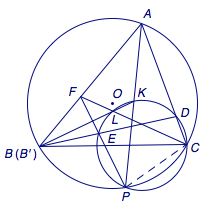对圆内接广义六边形\(DCPELK\)应用帕斯卡定理可知，\(DC\)与\(KP\)的交点\(A\)、\(CL\)与\(PE\)的交点\(F\)、\(LK\)与\(ED\)的交点\(B'\)共线，因此\(B'\)是\(AF\)与\(ED\)的交点，即\(B'=B\)，所以\(B\)、\(K\)、\(L\)共线． 根据\(A\)、\(B\)、\(P\)、\(C\)四点共圆及\(L\)、\(K\)、\(P\)、\(C\)四点共圆，得\[\angle ABC=\angle APC=\angle KLC=\angle FCB+\angle LBC,\]又由\(BK\)平分\(\angle ABC\)知\[\angle ABC=2\angle LBC,\]从而\(\angle ABC=2\angle FCB\)．

四、（本题共50分） 对正整数\(m\)，设\(v_2(m)\)表示正整数\(m\)的标准分解中素因子\(2\)的方幂，则熟知\[\begin{eqnarray}v_2(m!)=m-S(m),\end{eqnarray}\]这里\(S(m)\)表示正整数\(m\)在二进制表示下的数码之和． 由于\(2^{(k-1)n+1}\)不整除\(\dfrac{(kn)!}{n!}\)等价于\[v_2\left(\dfrac{(kn)!}{n!}\right)\leqslant (k-1)n,\]即\[kn-v_2\left((kn)!\right)\geqslant n-v_2\left(n!\right),\]进而由(5)知，本题等价于求所有正整数\(k\)，使得\(S(kn)\geqslant S(n)\)对任意正整数\(n\)成立． 我们证明，所有符合条件的\(k\)为\(2^a\)，其中\(a=0,1,2,\cdots\)． 一方面，由于\(S\left(2^an\right)=S(n)\)对任意正整数\(n\)成立，故\(k=2^a\)符合条件． 另一方面，若\(k\)不是\(2\)的方幂，设\(k=2^a\cdot q\)，\(a\geqslant 0\)，\(q\)是大于\(1\)的奇数． 下面构造一个正整数\(n\)，使得\(S(kn)<S(n)\)．因为\[S(kn)=S\left(2^aqn\right)=S(qn),\]因此问题等价于我们选取的\(q\)的一个倍数\(m\)，使得\[S(m)<S\left(\dfrac{m}{q}\right).\] 由\((2,q)=1\)，熟知存在正整数\(u\)，使得\(2^u\equiv 1\pmod q\)．（事实上，由欧拉定理知，\(u\)可以取\(\varphi(q)\)．） 设奇数\(q\)的二进制表示为\[2^{\alpha_1}+2^{\alpha_2}+\cdots+2^{\alpha_t},\]其中\(0=\alpha_1<\alpha_2<\cdots<\alpha_t\)，\(t\geqslant 2\)． 取\(m=2^{\alpha_1}+2^{\alpha_2}+\cdots+2^{\alpha_t+tu}\)，则\(S(m)=t\)，且\[m=q+2^{\alpha_t}\left(2^{tu}-1\right)\equiv 0\pmod q.\] 我们有\[\begin{eqnarray}\begin{split}\dfrac mq&=1+2^{\alpha_t}\cdot\dfrac{2^{tu}-1}{q}\\&=1+2^{\alpha_t}\cdot\dfrac{2^u-1}{q}\left(1+2^u+\cdots+2^{(t-1)u}\right)\\&=1+\sum_{i=0}^{t-1}\dfrac{2^u-1}{q}\cdot2^{iu+\alpha_t}.\end{split}\end{eqnarray}\] 由于\(0<\dfrac{2^u-1}q<2^u\)，故正整数\(\dfrac{2^u-1}{q}\)的二进制表示中的最高次幂小于\(u\)，由此可得，对任意整数\(i,j\)（\(0\leqslant i<j\leqslant t-1\)），数\(\dfrac{2^u-1}q\cdot 2^{iu+\alpha_t}\)与\(\dfrac{2^u-1}q\cdot 2^{ju+\alpha_t}\)的二进制表示中没有相同的项． 又因为\(\alpha_t>0\)，故\(\dfrac{2^u-1}q\cdot 2^{iu+\alpha_t}\)（\(i=0,1,2,\cdots,t-1\)）的二进制表示中均不包含\(1\)，故由(6)可知\[S\left(\dfrac mq\right)=1+S\left(\dfrac{2^u-1}q\right)\cdot t>t=S(m),\]因此上述选取的\(m\)满足要求． 综合上述的两个方面可知，所求\(k\)为\(2^a\)，其中\(a=0,1,2,\cdots\)．

点击此处下载pdf．