全卷共15道题,考试时间共3个小时.所有的答案都是$000$到$999$(包括$000$和$999$)之间的整数.
1、Initially Alex, Betty, and Charlie had a total of $444$ peanuts. Charlie had the most peanuts, and Alex had the least. The three numbers of peanuts that each person had form a geometric progression. Alex eats $5$ of his peanuts, Betty eats $9$ of her peanuts, and Charlie eats $25$ of his peanuts. Now the three numbers of peanuts that each person has form an arithmetic progression. Find the number of peanuts Alex had initially.
Alex,Betty和Charlie共有$444$颗花生,Alex的花生最少,Charlie的花生最多.三个人的花生数构成一个等比数列.Alex吃掉$5$颗花生,Betty吃掉$9$颗花生,Charlie吃掉$25$颗花生之后,三个人的花生数构成一个等差数列.求刚开始的时候Alex的花生数.
2、There is a $40\%$ chance of rain on Saturday and a $30\%$ of rain on Sunday. However, it is twice as likely to rain on Sunday if it rains on Saturday than if it does not rain on Saturday. The probability that it rains at least one day this weekend is $\dfrac{a}{b}$, where $a$ and $b$ are relatively prime positive integers. Find $a+b$.
已知周六的降雨概率为$40 \%$,周日的降雨概率为$30 \%$,周六降雨的条件下周日降雨概率是周六不降雨的条件下周日降雨概率的$2$倍.设周六周日两天至少有一天下雨的概率为$\dfrac{a}{b} $,其中$a,b$为互质的正整数.求$a+b$的值.
3、Let $x,y$ and $z$ be real numbers satisfying the system \begin{align*}
\log_2(xyz-3+\log_5 x) &= 5 \\
\log_3(xyz-3+\log_5 y) &= 4 \\
\log_4(xyz-3+\log_5 z) &= 4.
\end{align*}Find the value of $|\log_5 x|+|\log_5 y|+|\log_5 z|$.
已知实数$x,y,z$满足方程组$$\begin{cases}\log _2 \left (xyz-3+\log _5 x\right )=5,\\ \log _3 \left (xyz-3+\log _5 y\right )=4, \\ \log _4 \left (xyz-3+\log _5 z\right )=4. \end{cases} $$求$\left |\log_5x \right |+\left |\log_5y \right |+\left |\log_5z \right |$的值.
4、An $a\times b\times c$ rectangular box is built from $a\cdot b \cdot c$ unit cubes. Each unit cube is colored red, green, or yellow. Each of the $a$ layers of size $1\times b \times c$ parallel to the $(b\times c)$-faces of the box contains exactly $9$ red cubes, exactly $12$ green cubes, and some yellow cubes. Each of the $b$ layers of size $a\times 1 \times c$ parallel to the $(a\times c)$-faces of the box contains exactly $20$ green cubes, exactly $25$ yellow cubes, and some red cubes. Find the smallest possible volume of the box.
$a\cdot b \cdot c$个体积为$1$的单位正方体拼成一个尺寸为$a\times b \times c$的长方体,每个单位正方体的表面都涂上了红色、黄色或者绿色当中的某一种颜色.和“$b \times c$面”平行(尺寸为$1 \times b \times c$)的每一个“$a$层”都恰好有$9$个红色单位正方体、$12$个绿色单位正方体以及若干个黄色单位正方体;和“$a \times c$面”平行(尺寸为$a \times 1 \times c$)的每一个“$b$层”都恰好有$25$个黄色单位正方体、$20$个绿色单位正方体以及若干个红色单位正方体.求该长方体体积的最小值.
5、Triangle $ABC_0$ has a right angle at $C_0$. Its side lengths are pairwise relatively prime positive integers, and its perimeter is $p$. Let $C_1$ be the foot of the altitude to $\overline{AB}$, and for $n\geqslant 2$, let $C_n$ be the foot of the altitude to $\overline{C_{n-2}B}$ in $\triangle C_{n-2}C_{n-1}B$. The sum $\sum\limits_{n=1}^{\infty}C_{n-1}C_n = 6p$. Find $p$.
直角三角形$ABC_0$($C_0$为直角)的三边长是两两互质的正整数,周长为$p$.作$C_0C_1 \perp AB$于$C_1$,当$n \geqslant 2$时,作$C_{n-1}C_{n} \perp BC_{n-2}$于$C_n$.已知$\sum \limits_{n=1}^{\infty}C_{n-1}C_n=6p$,求$p$的值.
6、For polynomial $P(x)=1-\dfrac{1}{3}x+\dfrac{1}{6}x^2$, define $$ Q(x) = P(x)P(x^3)P(x^5)P(x^7)P(x^9) = \sum\limits_{i=0}^{50}a_ix^i. $$Then $\sum\limits_{i=0}^{50}|a_i|=\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
已知多项式$P(x)=1-\dfrac{1}{3}x+\dfrac{1}{6}x^2 $,定义$$Q(x)=P(x)P(x^3)P(x^5)P(x^7)P(x^9)=\sum _{i=0}^{50}a_ix^i.$$
设$\sum \limits_{i=0}^{50}|a_i|=\dfrac{m}{n} $,其中$m,n$为互质的正整数.求$m+n$的值.
7、Squares $ABCD$ and $EFGH$ have a common center and $\overline{AB}\parallel \overline{EF}$. The area of $ABCD$ is $2016$, and the area of $EFGH$ is a smaller positive integer. Square $IJKL$ is constructed so that each of its vertices lies on a side of $ABCD$ and each vertex of $EFGH$ lies on a side of $IJKL$. Find the difference between the largest and smallest possible integer values of the area of $IJKL$.
正方形$ABCD$的面积为$2016$,正方形$IJKL$的$4$个顶点分别落在正方形$ABCD$的$4$条边上,其面积为正整数.正方形$EFGH$的$4$个顶点分别落在正方形$IJKL$的$4$条边上,其中心与正方形$ABCD$的中心重合,$EF \parallel AB$,且其面积是一个小于$2016$的正整数.求正方形$IJKL$面积的最大值与最小值的差.
8、Find the number of sets $\{a,b,c\}$ of three distinct positive integers with the property that the product of $a,b,$ and $c$ is equal to the product of $11,21,31,41,51,$ and $61$.
$a,b,c$是三个不同的正整数,$abc=11\cdot 21 \cdot 31 \cdot 41\cdot 51\cdot 61$.求所有满足要求的集合$\{ a,b,c \}$的个数.
9、The sequences of positive integers $1,a_2,a_3,\cdots$ and $1,b_2,b_3,\cdots$ are an increasing arithmetic sequence and an increasing geometric sequence, respectively. Let $c_n=a_n+b_n$. There is an integer $k$ such that $c_{k-1}=100$ and $c_{k+1}=1000$. Find $c_k$.
$1,a_2,a_3,\cdots$是一个各项均为正整数的单调递增的等差数列,$1,b_2,b_3,\cdots$是一个各项均为正整数的单调递增的等比数列.令$c_n=a_n+b_n$,已知存在整数$k$满足$c_{k-1}=100,c_{k+1}=1000$,求$c_k$的值.
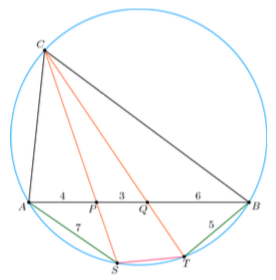
10、Triangle $ABC$ is inscribed in circle $\omega$. Points $P$ and $Q$ are on side $\overline{AB}$ with $AP<AQ$. Rays $CP$ and $CQ$ meet $\omega$ again at $S$ and $T$ (other than $C$), respectively. If $AP=4,PQ=3,QB=6,BT=5,$ and $AS=7$, then $ST=\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
三角形$ABC$内接于圆$\omega$,$P,Q$是线段$AB$上的点,且$AP<AQ$.射线$CP,CQ$分别交圆$\omega$于点$S,T$.如果$AP=4,PQ=3,QB=6,BT=5,AS=7$,设$ST=\dfrac{m}{n}$,其中$m,n$为互质的正整数.求$m+n$的值.
11、For positive integers $N$ and $k$, define $N$ to be $k$-nice if there exists a positive integer $a$ such that $a^k$ has exactly $N$ positive divisors. Find the number of positive integers less than $1000$ that are neither $7$-nice nor $8$-nice.
对于正整数$N,k$,若存在正整数$a$,使得$a^k$恰好有$N$个正因数,则称$N$是一个“$k$-好数”.求小于$1000$的正整数中,既不是“$7$-好数”又不是“$8$-好数”的正整数的个数.
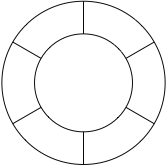
12、The figure below shows a ring made of six small sections which you are to paint on a wall. You have four paint colors available and will paint each of the six sections a solid color. Find the number of ways you can choose to paint each of the six sections if no two adjacent section can be painted with the same color.
用$4$种不同的颜色给下图中的$6$个扇环染色,每个扇环只染一种颜色,相邻的扇环染不同的颜色,求所有染色的方法数.
13、Beatrix is going to place six rooks on a $6\times6$ chessboard where both the rows and columns are labelled $1$ to $6$; the rooks are placed so that no two rooks are in the same row or the same column. The value of a square is the sum of its row number and column number. The score of an arrangement of rooks is the least value of any occupied square. The average score over all valid configurations is $\dfrac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.
Beatrix在一个$6\times6$的棋盘上放了$6$枚棋子,任意两枚棋子既不在同一行也不在同一列.定义某一枚棋子的分值为其所在位置的行数与列数之和,定义$6$枚棋子的总分值为这$6$枚棋子分值的最小值.将所有排列中$6$枚棋子的总分值的平均数记为$\dfrac{p}{q}$,其中$p,q$为互质的正整数.求$p+q$的值.
14、Equilateral $\triangle ABC$ has side length $600$. Points $P$ and $Q$ lie outside of the plane of $\triangle ABC$ and are on the opposite sides of the plane. Furthermore, $PA=PB=PC$, and $QA=QB=QC$, and the planes of $\triangle PAB$ and $\triangle QAB$ form a $120^{\circ}$ dihedral angle (The angle between the two planes). There is a point $O$ whose distance from each of $A,B,C,P$ and $Q$ is $d$. Find $d$.
等边三角形$\triangle ABC$的边长为$600$.点$P$,$Q$在平面$ABC$的外面,并且分别位于平面$ABC$的两侧.$PA=PB=PC$,$QA=QB=QC$,二面角$P-AB-Q$的大小为$120^{\circ}$.若点$O$到点$A,B,C,P,Q$的距离均等于$d$,求$d$的值.
15、For $1\leqslant i\leqslant 215$ let $a_i=\dfrac{1}{2^i}$ and $a_{216}=\dfrac{1}{2^{215}}$. Let $x_1,x_2,\cdots,x_{216}$ be positive real numbers such that $$ \sum\limits_{i=1}^{216} x_i=1 \ and\ \sum\limits_{1\leqslant i<j \leqslant 216} x_ix_j = \dfrac{107}{215}+ \sum\limits_{i=1}^{216} \dfrac{a_ix_i^2}{2(1-a_i)}.$$The maximum possible value of $x_2=\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
已知$a_i=\dfrac{1}{2^i}(i=1,2,\cdots ,215)$,$a_{216}=\dfrac{1}{2^{215}}$.正实数$x_1,x_2,\cdots,x_{216}$满足$$\sum\limits_{i=1}^{216} x_i=1,\quad \sum\limits_{1\leqslant i<j \leqslant 216} x_ix_j = \dfrac{107}{215}+ \sum\limits_{i=1}^{216} \dfrac{a_ix_i^2}{2(1-a_i)}.$$
设$x_2$的最大值为$\dfrac{m}{n}$,其中$m,n$为互质的正整数.求$m+n$的值.
参考答案
1、$108$.
由题意,设刚开始的时候Alex的花生数为$x$,Betty的花生数为$xq$,Charlie的花生数为$xq^2$,则
$$\begin{cases}x+xq+xq^2=444,\\ x-5+xq^2-25=2(xq-9),\end{cases} $$
解得$$\begin{cases}x=108,\\ q=\dfrac{4}{3}. \end{cases} $$注 吃掉一些花生后的等差数列的排列有多种可能,讨论知只有顺序不变时有解.
2、$107$.
设事件$A$表示周六降雨,事件$B$表示周日降雨,则$P(A)=0.4,P(B)=0.3$,故$$P(B|A)=\dfrac{P(AB)}{P(A)} =2P\left (B|\overline{A}\right )=\dfrac{2P\left (\overline{A}B \right )}{P\left (\overline{A}\right )} ,$$
解得$P\left (\overline{A}B \right )=\dfrac{9}{70} $.
所以周六周日两天至少有一天下雨的概率为$$P(AB)+P\left (A\overline{B} \right )+P\left (\overline{A}B \right )=P(A)+P\left (\overline{A}B \right )=\dfrac{37}{70} .$$
3、$265$.
设$a=\log_5x,b=\log_5y,c=\log_5z$,则$$\begin{cases}5^{a+b+c}+a=35,\\ 5^{a+b+c}+b=84,\\5^{a+b+c}+c=259, \end{cases} $$
以上三式相加,可得$3\cdot 5^{a+b+c}+(a+b+c)=378$,所以$a+b+c=3$,进而可解得$$\begin{cases}a=-90,\\ b=-41,\\ c=134.\end{cases} $$
4、$180$.
设每一个“$a$层”都恰好有$x$个黄色单位正方体,每一个“$b$层”都恰好有$y$个红色单位正方体.由题意,可得$$\begin{cases}9a=yb,\\ xa=25b,\\ 12a=20b,\end{cases} $$解得$$\begin{cases}3a=5b,\\ x=15,\\y=15.\end{cases} $$
故该长方体的体积$V=36a \geqslant 180$,易知,等号可以取到.
5、$182$.
设$C_0C_1$的长为$h$.因为$\sum \limits_{n=1}^{\infty}C_{n-1}C_n=6p$,所以$$\dfrac{h}{1-\sin A} =6h\left (\dfrac{1}{\sin A}+\dfrac{1}{\cos A}+\tan A+\cot A \right ),$$整理得$7\sin A-6\cos A=6$,解得$\cos A=\dfrac{13}{85} $($\cos A=-1$舍去).
所以$p=13+84+85=182$.
6、$275$.
$\sum \limits_{i=0}^{50}|a_i|=Q(-1)=\left (\dfrac{3}{2}\right )^5= \dfrac{243}{32} $.
7、$840$.
由题意,设正方形$ABCD$的面积为$S_1=2016$,正方形$IJKL$的面积为$S_2=2016q$,正方形$EFGH$的面积为$S_3=2016q^2$,其中$\dfrac{1}{2}\leqslant q <1 $.
显然,正方形$IJKL$面积的最小值为$1008$.
因为$S_1S_3=12^2\cdot 14S_3=S_2^2$为完全平方数,故$S_3=14m^2$,其中$m$为正整数.
所以$S_2=12\cdot 14m$,由此可得$q=\dfrac{m}{12} \leqslant \dfrac{11}{12} $.
经检验,当$q=\dfrac{11}{12} $时满足题意,所以正方形$IJKL$面积的最大值为$1848$.
8、$728$.
由题意,$abc=11\cdot 3 \cdot 7 \cdot 31 \cdot 41\cdot 3 \cdot 17 \cdot 61$.先考虑$11,7,31,41,17,61$这$6$个素数,它们“分配”给$a,b,c$的方式共有$3^6=729$种.
接下来考虑两个$3$,它们“分配”给$a,b,c$的方式共有$\mathrm C _4^2=6$种.
导致$a,b,c$三个数中有相同数的方法共有$2\mathrm C _3^2=6$(有两个数等于$1$或有两个数等于$3$)种.
考虑到集合元素的互异性和无序性,所有满足要求的集合$\{ a,b,c \}$的个数应为$\dfrac{3^6\cdot \mathrm C _4^2-2\mathrm C _3^2}{\mathrm A_3^3}=728 $.
9、$262$.
由题意,设$a_n=1+(n-1)d$,其中$d$是正整数;$b_n=q^{n-1}$,其中$q$是大于等于$2$的正整数.
若$q\geqslant 10$,容易推出与题意不符.
若$q \leqslant 9$,逐一验证可知,当且仅当数列$\{ a_n \}$为$1,91,181,271,\cdots$,数列$\{ b_n \}$为$1,9,81,729,\cdots$,$k=3$时满足题意.
10、$043$.
方法一
如图,由射影几何中的Chasles定理可知,$$(CA,CT;CS,CB)=(A,T;S,B)=(A,Q;P,B),$$所以$ST=\dfrac{35}{8}$.
方法二
如图,因为\[\begin{split}\dfrac{AP\cdot QB \cdot ST}{AS\cdot BT \cdot PQ}&=\dfrac{AP}{AS}\cdot \dfrac{QB}{BT}\cdot \dfrac{ST}{PQ} \\&= \dfrac{AP}{AS}\cdot \dfrac{QC}{CA}\cdot \dfrac{ST}{PQ} \\&=\dfrac{AP}{CA}\cdot \dfrac{QC}{PQ}\cdot \dfrac{ST}{AS}\\&=\dfrac{\sin \angle ACP}{\sin \angle APC}\cdot \dfrac{\sin \angle CPQ}{\sin \angle PCQ}\cdot \dfrac{\sin \angle PCQ}{\sin \angle ACP} \\&=1,\end{split} \]
所以$ST=\dfrac{35}{8}$
11、$749.$
易知,$k$-好数是模$k$余$1$的数.
在小于$1000$的正整数中,“$7$-好数”有$1,8,\cdots,995$,共$143$个;“$8$-好数”有$1,9,\cdots,993$,共$125$个;“$56$-好数”有$1,57,\cdots,953$,共$18$个.
所以在小于$1000$的正整数中,既不是“$7$-好数”又不是“$8$-好数”的正整数的个数为$999-143-125+18=749$.
12、$732.$
一般的,我们来考虑用$k$种不同的颜色给$n$个扇环染色的方法数$a_n$.
方法一$$a_n+a_{n-1}=k\cdot (k-1)^{n-1},\quad a_1=0,\quad a_2=k(k-1),$$
解得$$a_n=(k-1)^n+(k-1)\cdot (-1)^n.$$
方法二$$a_n=(k-2)a_{n-1}+(k-1)a_{n-2},\quad a_1=0,\quad a_2=k(k-1),$$
解得$$a_n=(k-1)^n+(k-1)\cdot (-1)^n.$$
13、$371.$
将$6$枚棋子的总分值记为随机变量$X$.
(1)$X\geqslant 2$的情况有$6!=720$种.
(2)$X\geqslant 3$的情况有$5\cdot 5!=600$种.
(3)$X\geqslant 4$的情况有$4^2\cdot 4!=384$种.
(4)$X\geqslant 5$的情况有$3^3\cdot 3!=162$种.
(5)$X\geqslant 6$的情况有$2^4\cdot 2!=32$种.
(6)$X=7$的情况有$1$种.
综上所述,所有排列中$6$枚棋子的总分值的平均数为$$E(X)=\sum\limits_{k=1}^{\infty}P(X\geqslant k)=\dfrac{720+720+600+384+162+32+1}{6!}=\dfrac{291}{80}. $$
注 若$X$是取非负整数值的随机变量,则$$E(X)=\sum\limits_{k=1}^{\infty}P(X\geqslant k).$$
14、$450.$
设$G$是$\triangle ABC$的中心,$M$是线段$AC$的中点,则$\angle PAQ=90^{\circ},\angle PMQ=120^{\circ}$.
设$GM=a=100\sqrt{3},PM=x,QM=y$.
在$\triangle PMQ$中,有$$PQ^2=x^2+y^2+xy,$$
在$\triangle PAQ$中,有$$PQ^2=AP^2+AQ^2=2AM^2+PM^2+QM^2=6a^2+x^2+y^2,$$
故$$xy=6a^2.$$
在$\triangle PMQ$中,由$$2S_{\triangle PMQ}=xy\sin \angle PMQ=PQ\cdot GM,$$
可知$PQ=3\sqrt{3}a=900 $.所以$$d=\dfrac12 PQ=450.$$
15、$863.$
由题意,$$1=\left (\sum\limits_{i=1}^{216} x_i \right )^2=\sum\limits_{i=1}^{216} x_i^2 +2 \sum\limits_{1\leqslant i<j \leqslant 216} x_ix_j =\sum\limits_{i=1}^{216} x_i^2+\dfrac{214}{215}+ \sum\limits_{i=1}^{216} \dfrac{a_ix_i^2}{1-a_i}=\dfrac{214}{215}+ \sum\limits_{i=1}^{216} \dfrac{x_i^2}{1-a_i},$$
所以$\sum\limits_{i=1}^{216} \dfrac{x_i^2}{1-a_i}=\dfrac{1}{215} $.
由柯西不等式,$$1=\sum\limits_{i=1}^{216}\left (1-a_i \right ) \cdot \sum\limits_{i=1}^{216} \dfrac{x_i^2}{1-a_i}\geqslant \left (\sum\limits_{i=1}^{216} x_i \right )^2=1,$$
故$$\dfrac{x_1}{1-a_1}=\dfrac{x_2}{1-a_2}=\cdots=\dfrac{x_{216}}{1-a_{216}}= \dfrac{\sum\limits_{i=1}^{216} x_i}{\sum\limits_{i=1}^{216} \left (1-a_i \right )}=\dfrac{1}{215}, $$
所以$$x_2=\dfrac{1-a_2}{215}=\dfrac{3}{860} .$$