1、$\triangle ABC$的内点$M$满足$\angle CMB=100^\circ$，线段$BM$的中垂线交边$AB$于$P$，线段$CM$的中垂线交边$AC$于$Q$．已知$P$、$M$、$Q$三点共线，求$\angle CAB$．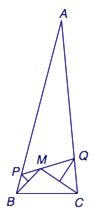 
2、正数$a,b,c$满足$a<b+c$，求证：$\dfrac{a}{1+a}<\dfrac{b}{1+b}+\dfrac{c}{1+c}$．
3、是否存在互不相同的三个实数$a,b,c$，使平面直角坐标系中的三条直线$y=ax+b$，$y=bx+c$，$y=cx+a$共点．
4、若$\{1,2,\cdots ,9\}$的某非空子集中所有元素的和为奇数，则称之为奇子集．求奇子集的个数．
5、在一个$2013\times 2013$的正数数表中，每行都成等差数列，每列平方后都成等差数列．求证：左上角的数和右下角的数之积等于左下角的数和右上角的数之积．
参考答案
1、由$\angle BMC=100^\circ$，知$$\angle PBM + \angle QCM = \angle PMB + \angle QMC = 180^\circ - \angle BMC = 80^\circ,$$而$$\angle MBC + \angle MCB = 180^\circ - \angle BMC = 80^\circ,$$于是$$\angle ABC + \angle ACB = \left( {\angle PBM + \angle QCM} \right) + \left( {\angle MBC + \angle MCB} \right) = 160^\circ ,$$从而$\angle BAC = 20^\circ $．
2、可以直接放缩$$\begin{split} \dfrac{a}{{1 + a}} &= \dfrac{1}{{\dfrac{1}{a} + 1}}\\& < \dfrac{1}{{\dfrac{1}{{b + c}} + 1}} \\&= \dfrac{{b + c}}{{b + c + 1}}\\&= \dfrac{b}{{b + c + 1}} + \dfrac{c}{{b + c + 1}} \\&< \dfrac{b}{{1 + b}} + \dfrac{c}{{1 + c}},\end{split} $$因此原不等式得证．
3、原问题即方程组$ax + b = bx + c = cx + a$有解$\left( {a , b , c , x} \right)$，其中$a , b , c$两两不同．事实上，由$$ax + b = bx + c = cx + a$$可得$$x = \dfrac{{c-b}}{{a-b}} = \dfrac{{a-c}}{{b-c}},$$整理右边等式得$${a^2} + {b^2} + {c^2} = ab + bc + ca,$$即$$\dfrac 12\sum_{cyc}{(a-b)^2}=0,$$与$a , b , c$两两不同矛盾，于是不存在符合题意的实数对$\left( {a , b , c} \right)$．
4、设$M = \left\{ {1 , 3 , 5 , 7 , 9} \right\}$，$N = \left\{ {2 , 4 , 6 , 8} \right\}$，则奇子集由$M$中的$1$个、$3$个或$5$个元素以及$N$中的任意个元素组成．因此奇子集个数为$$\left( {{\rm {C}}_5^1 + {\rm {C}}_5^3 + {\rm {C}}_5^5} \right) \cdot {2^4} = 256.$$
5、下面证明对$n \times n$的数表，其中$n \geqslant 3 $，$n \in {\mathcal{N}^ * }$，$n$是奇数，命题均成立．
当$n = 2k + 1$时，不妨设数表如下$$\begin{array} &a&\cdots &\dfrac{a+b}2&\cdots &b\\\cdots &\cdots &\cdots &\cdots &\cdots \\\sqrt{ \dfrac{a^2+c^2}2}&\cdots &\sqrt {\dfrac{\left( \frac{a+b}2\right)^2+\left(\frac{c+d}2\right) ^2}{2}}&\cdots &\sqrt{\dfrac{b^2+d^2}2}\\\cdots &\cdots &\cdots &\cdots &\cdots \\c&\cdots &\dfrac{c+d}2&\cdots &d\end{array}$$于是$$\begin{split}&\quad 2\sqrt {\dfrac{{{{\left( {\frac{{a + b}}{2}} \right)}^2} + {{\left( {\frac{{c + d}}{2}} \right)}^2}}}{2}} = \sqrt {\dfrac{{{a^2} + {c^2}}}{2}} + \sqrt {\dfrac{{{b^2} + {d^2}}}{2}} \\& \Leftrightarrow {\left( {a + b} \right)^2} + {\left( {c + d} \right)^2} = {a^2} + {c^2} + {b^2} + {d^2} + 2\sqrt {\left( {{a^2} + {c^2}} \right)\left( {{b^2} + {d^2}} \right)} \\& \Leftrightarrow {\left( {ab + cd} \right)^2} = \left( {{a^2} + {c^2}} \right)\left( {{b^2} + {d^2}} \right)\\&\Leftrightarrow 2abcd = {b^2}{c^2} + {a^2}{d^2}\\&\Leftrightarrow ad = bc,\end{split} $$因此命题成立．