2013年北京大学暑期体验营数学试题

1、凸五边形$ABCDE$满足$AB=AE=DC=BC+DE=1$，$\angle B=\angle E=90^\circ$，求这个五边形的面积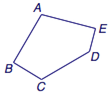． 2、设$f(x)=2x^2-ax+7$，已知存在$\varphi\in \left( \dfrac {\pi} 4,\dfrac {\pi} 2\right) $，满足$f(\sin \varphi)=f(\cos \varphi)$，求参数$a$的取值范围．

3、函数$y=ax^2+bx+c$的图象与坐标轴交于三个不同的点$A$、$B$、$C$，已知三角形$ABC$的外心在直线$y=x$上，求$a+b$的值．

4、设等差数列$\{a_n\}$的前$14$项和$a_1+a_2+\cdots+a_{14}=77$，已知$a_1$，$a_{11}$为正整数，求$a_{18}$的值．

5、一个班有$n$个同学，每个同学都有一个信息希望通过短信告诉别人．已知每次一个同学可以给另一个同学告诉他自己已经知道的所有信息．若需要使每个同学都知道所有的信息，那么同学们需要发送短信条数的总和的最小值是多少？

参考答案

1、如图，将五边形$ABCDE$沿$AC$和$AD$分割为三个部分，然后将$\triangle ADE$旋转至$\triangle AFB$，则由已知，$F$、$B$、$C$三点共线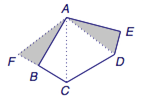． 于是$$\begin{split} S_{ABCDE}&=S_{\triangle AFC}+S_{\triangle ADC}\\&=2S_{\triangle ABC}=1.\end{split} $$

2、将$\sin\varphi$和$\cos\varphi$分别代入$f(x)$的解析式，并由$f(\sin\varphi)=f(\cos\varphi)$整理得$$\dfrac 12 \left( {\sin\varphi+\cos\varphi}\right) =\dfrac a4,$$即$$a=2\sqrt 2\sin\left(\varphi+\dfrac {\pi} 4\right) ,$$又$\varphi\in\left(\dfrac {\pi} 4,\dfrac {\pi} 2\right) $，因此$a$的取值范围是$\left( 2,2\sqrt 2\right) $．

3、显然圆心的坐标为$M \left( -\dfrac a2,-\dfrac a2\right) $，于是对原点$O$应用圆幂定理有$$\overrightarrow {OA}\cdot \overrightarrow {OB}=OM^2-MC^2,$$即$$b=\left(-\dfrac a2\right)^2+\left(-\dfrac a2\right)^2-\left[\left(-\dfrac a2\right) ^2+ \left( -\dfrac a2-b\right)^2\right],$$整理即得$$a+b=-1.$$

4、根据题意，有$$\sum_{k=1}^{14}a_k=7(a_1+a_{14})=77,$$于是$$a_1+a_{14}=11,$$从而$$a_{11}=a_1+10\cdot\dfrac{11-2a_1}{13}=\dfrac{110-7a_1}{13},$$由于$a_1,a_{11}$均为正整数，于是可以解得$$(a_1,a_{11})=(12,2),$$于是$$a_{18}=a_1+\dfrac{17}{10}\cdot (a_{11}-a_1)=-5.$$

5、最小的短信条数总数为$2n-2$． 对每个人而言，至少需要对外发一条短信告知自己的信息，共$n$条．而这$n$条短信至多只能让$2$个人获得所有信息，此时还需要$n-2$条短信去通知剩余的同学，于是短信总数不少于$2n-2$． 另一方面，$n-1$名同学都将信息发送给最后一名同学，然后由这名同学再给$n-1$名同学回复，就可以用$2n-2$条短信完成任务． 综上，最小的短信条数总数为$2n-2$．