这是2014年北京市25校高三联考解析几何试题:
已知椭圆\(W:\dfrac {x^2}{2m+10}+\dfrac {y^2}{m^2-2}=1\)的左焦点为\(F(m,0)\),过点\(M(-3,0)\)作一条斜率大于\(0\)的直线\(l\)与椭圆\(W\)交于不同的两点\(A\)、\(B\),延长\(BF\)交椭圆\(W\)于点\(C\).
(1)求椭圆\(W\)的离心率;
(2)若\(\angle MAC=60^\circ\),求直线\(l\)的斜率.
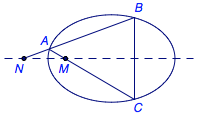
如图,若\(M(m,0)\),\(N(n,0)\)分别是椭圆\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)\)长轴所在直线上的两点,且\(mn=a^2\),则取椭圆上任意一点(不在长轴上)\(A(x_0,y_0)\),设直线\(AN\),\(AM\)与椭圆的另外一个交点分别为\(B(x_1,y_1)\),\(C(x_2,y_2)\),则\(y_1+y_2=0\).
设\(\overrightarrow{AM}=\lambda\overrightarrow{MC},\overrightarrow{AN}=\mu\overrightarrow{NB}\),则
\[M\left(\dfrac {x_0+\lambda x_1}{1+\lambda},\dfrac {y_0+\lambda y_1}{1+\lambda}\right),N\left(\dfrac {x_0+\mu x_2}{1+\mu},\dfrac {y_0+\mu y_2}{1+\mu}\right).\]
根据已知,有\[\dfrac {x_0+\lambda x_1}{1+\lambda}=m,y_0+\lambda y_1=0\\\dfrac {x_0+\mu x_2}{1+\mu}=n,y_0+\mu y_2=0.\]
由\[\dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}=1,\dfrac{(\lambda x)^2}{a^2}+\dfrac{(\lambda y)^2}{b^2}=\lambda^2\]两式相减,整理得
\[\dfrac {x_0+\lambda x_1}{1+\lambda}\cdot\dfrac {x_0-\lambda x_1}{1-\lambda}=a^2.\]
类似的,可得
\[\dfrac {x_0+\mu x_2}{1+\mu}\cdot\dfrac {x_0-\mu x_2}{1-\mu}=a^2.\]
结合\(mn=a^2\),可得 \(\lambda+\mu=0\),从而可得\(y_1+y_2=0\).
应用到本试题上,马上就可以得到直线\(l\)的斜率为\(\dfrac{\sqrt 3}3\).