- 选择题压轴
已知\(f(x)=\begin{cases}x^2-4x+3,&x\leqslant 0,\\-x^2-2x+3,&x>0.\end{cases}\)不等式\(f(x+a)>f(2a-x)\)在\([a,a+1]\)上恒成立,则实数\(a\)的取值范围是( )
A.\((-2,0)\)
B.\((-\infty,0)\)
C.\((0,2)\)
D.\((-\infty,-2)\)
- 填空题压轴
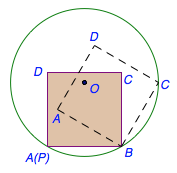
圆\(O\)的半径为\(1\),\(P\)为圆周上一点,现将如图放置的边长为\(1\)的正方形(实线所示,正方形的顶点\(A\)与\(P\)重合)沿圆周顺时针滚动,经过若干次滚动,点\(A\)第一次回到点\(P\)的位置,则点\(A\)走过的路径的长度为____.
- 解析几何大题
已知椭圆\(W:\dfrac {x^2}{2m+10}+\dfrac {y^2}{m^2-2}=1\)的左焦点为\(F(m,0)\),过点\(M(-3,0)\)作一条斜率大于\(0\)的直线\(l\)与椭圆\(W\)交于不同的两点\(A\)、\(B\),延长\(BF\)交椭圆\(W\)于点\(C\).
(1)求椭圆\(W\)的离心率;
(2)若\(\angle MAC=60^\circ\),求直线\(l\)的斜率.
- 导数大题
已知定义在\((1,+\infty)\)上的函数\(f(x)=x-\ln x-2\),\(g(x)=x\ln x+x\).
(1)求证:\(f(x)\)存在唯一的零点,且零点属于\((3,4)\);
(2)若\(k\in \mathbf Z\),且\(g(x)>k(x-1)\)对任意的\(x>1\)恒成立,求\(k\)的最大值.
- 组合大题
- 选择题压轴
注意到\(f(x)\)为单调函数,选D. - 填空题压轴
\(\dfrac {\pi}{6}\left(3\times 1+3\times \sqrt 2+3\times 1\right)=\pi\left(1+\dfrac {\sqrt 2}2\right)\). - 解析几何大题
注意到\(k_{AB}+k_{MC}=0\),于是斜率为\(\dfrac {\sqrt 3}3\). - 导数大题
分离变量,注意对其中对数函数的换元处理,估计最值.\(k\)的最大值为\(3\). - 组合大题
略