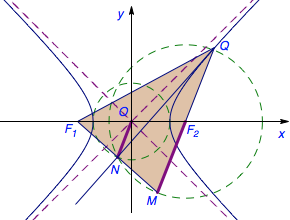
这是49周数学组功底测试的圆锥曲线试题:
已知焦点在\(x\)轴上的双曲线\(C\)的两条渐近线过坐标原点,且两条渐近线与以点\(A(0,\sqrt 2)\)为圆心,\(1\)为半径的圆相切.又知\(C\)的一个焦点与\(A\)关于直线\(y=x\)对称.
(1)求双曲线的方程;
(2)若\(Q\)是双曲线上的任一点,\(F_1\),\(F_2\)为双曲线的左、右两个焦点,从\(F_1\)引\(\angle F_1QF_2\)的平分线的垂线,垂足为\(N\),试求点\(N\)的轨迹方程.
(1)\(x^2-y^2=1\);
(2)\(x^2+y^2=1(x\neq -\dfrac {\sqrt 2}2)\).
仔细看看这张图,你就可以轻松得到结果了(注意利用极限思想确定图形缺少的点).